1. 서 론
캐비테이션은 액체 내에서 국부적인 압력이 해당 액체의 증기압보다 낮아지면서 기화 과정이 일어나는 현상을 의미한다. 이러한 캐비테이션은 터보기계, 수중익, 프로펠러, 열교환기, 밸브 등의 기계공학 분야는 물론이고 의공학, 주류발효, 토양개선, 박테리아 살균 등의 광범위한 영역에서 나타나며 그 기술이 활용되고 있다.
캐비테이션이 발생할 때 수반되는 마이크로 버블이 붕괴하는 과정에서 버블 경계에서의 압력 차에 의해 마이크로 제트(mirco jet)가 발생하고 그 속도는 수십에서 수천 m/s에 달할 수 있다. 고체 근처에서의 버블 붕괴는 마이크로 제트에 의한 강한 충격력을 벽면에 전달한다. 마이크로 버블 붕괴에 대한 연구는 터보기계, 수중익, 프로펠러, 열교환기, 밸브 등에서의 침식 방지 및 수명 예측과 같은 기계공학 분야뿐만 아니라, 비침습적 치료와 같은 의공학 분야, 주류 발효 과정의 효율 증진, 토양 개선을 통한 농업 생산성 향상, 그리고 박테리아 살균과 같은 화학, 생물학적 응용에 이르는 다양한 분야에서 중요한 역할을 하고 있다[1,2].
의공학 분야에서 활용되는 고강도 초음파 집속술(HIFU:High Intensity Focused Ultrasound)은 고압과 저압이 반복되는 국부적인 영역을 형성하여 치료목표에 축적된 마이크로버블 핵의 성장, 붕괴를 유발하며, 붕괴 시 발생하는 충격력에 의해 종양, 결석 등을 비침습적으로 파괴할 수 있다[3,4,5,6,7]. HIFU에 의해 버블이 형성되고 붕괴하는 과정에 대한 연구는 기초적인 단계에 머물러 있으며, 변화하는 압력장에 대한 모사부터 압력 변화에 의한 버블의 성장, 붕괴 과정에서의 상변화에 대한 정확한 예측 등을 필요로 하는 도전적인 연구주제이다.
신장결석에 부착되는 마이크로 버블의 타겟팅 기술과 파괴 효과에 대한 Marchall L. Stoller 등[4]의 연구를 바탕으로 Daniel J. Laser 등[5,6]은 시험관 내 결석 표면의 마이크로버블 역학에 대한 실험 및 다성분 오일러 방정식(multicomponent Euler equations)기반 수치해석 연구를 수행하였다. 해당 연구에서는 1 MHz 진폭의 HIFU를 통해 신장결석의 표면에 축적되도록 설계된 Stone-Surface-Accumulating(SSA) 마이크로버블은 최대 확장 시 그 단면이 결석에 의해 잘린 타원형(oblate spheroid)구체로 나타나는 것을 확인하였으며, 초기 버블 내부압력에 따른 붕괴 특성을 비교하였다.
마이크로 버블핵의 점착 정도, 벽의 특성 등 다양한 요인에 따라, 벽면으로부터의 거리가 불규칙하게 형성될 수 있으며, 이는 버블의 붕괴 특성에 중요한 영향을 미친다. 그러나 벽면에 부착된 버블의 형성 거리가 붕괴 특성에 미치는 영향에 관한 연구는 거의 이루어지지 않았다.
본 연구에서는 HIFU(High-Intensity Focused Ultrasound)에 의해 벽면에 부착되어 형성된 타원형 버블의 생성 및 붕괴 과정에 대해 Daniel J. Laser 등[5]이 수행한 실험 및 전산해석 연구결과를 기반으로, 압축성 축대칭 나비에-스톡스(Navier-Stokes) 방정식을 사용하는 균일 혼상류 모델(Homogeneous mixture)을 활용하여 버블 중심으로부터 벽면까지 수직거리로 정의되는 이격거리(stand-off distance)에 따른 버블 붕괴 현상을 수치해석하였다. 압력장 및 벽면에서의 압력상승, 마이크로 제트 속도 등의 결과를 통해 붕괴 시 나타나는 형상적 특성과 벽면에 미치는 압력상승의 경향성을 분석하였다. 버블과 벽면 사이의 거리가 붕괴 특성에 미치는 영향을 분석함으로써, 벽면에 가해지는 충격력에 대한 기초적인 이해를 얻을 수 있다.
2. 지배 방정식
본 연구에서 사용된 자체 개발 수치해석 코드(in-house code)는 FORTRAN 프로그래밍 언어로 구현되었으며, 이전 연구를 통해 다양한 조건에서 신뢰성이 이미 검증되었다[9,10,11,12,13,14].
벽 근처에 발생하는 타원형 버블의 붕괴과정에 대한 수치해석을 위해 2상 유동에 대한 열 및 질량전달을 고려한 Navier-Stokes 기반 완전 압축성 균일 혼상류 모델을 사용하였다. 마이크로 버블의 붕괴와 같이 액상(liquid)과 기상(vapor)이 혼재하는 물리적 현상에 대한 수치해석을 위해서는 다상유동(multi phase flow)을 처리할 수 있는 해석기법이 필요하다. 본 논문의 전산해석에서 사용된 다상유동 해석 기법 균일혼상류모델(homogenous mixture model)[8]은 상 경계에서 관성력 차이에 의한 미끄럼 속도가 없고 열적으로 평형이라는 가정하에 혼상류에 대한 지배방정식을 풀어 해를 구하기 때문에 상대적으로 적은 방정식의 풀이를 요구하여 계산 시간을 단축시킬 수 있다는 장점을 가지고 있다. 버블은 기상으로만 이루어지며, 다른 상은 액체인 것으로 가정하였다.
Navier-Stokes방정식을 지배 방정식으로 하며 유체를 균질 혼합류(mixture flow)로 가정함으로서 개별 상에 대한 질량 보존 방정식과 증기-액체 혼합류 상에 대한 운동량 보존 방정식과 에너지 보존 방정식을 포함한다. 응축과 증발을 포함한 물질 전달 과정의 모델링은 질량 보존 방정식의 소스항을 사용하여 수행한다. 열전달 과정은 국소 온도 구배에 의한 열 유속 항과 상변화에 의한 에너지의 변화를 위한 에너지 소스항에 의해 계산된다. 또한 버블 표면의 선명한 상경계면 유지를 위해 기체에 대한 추가 표면 이류(advection) 방정식을 채택하였다. 추가적으로, 수정된 이중시간(dual-time) 예조건화 기법[15]을 사용하여 상에 따른 Mach수 변화의 비정상(unsteady)문제에 대해 보다 정확한 결과를 얻을 수 있었다. 일반화된 곡선 좌표계에서 지배방정식은 다음과 같이 표현된다[15].
여기서 는 물리적 시간(physical time), 𝜏는 의사시간(pseudo time)를 의미하며, 𝜉, 𝜂, 𝜁는 해석 영역에서의 좌표를 나타낸다. 는 원시 변수벡터(primitive variable vector), , 와 는 대류 선속 벡터(convective flux vector), , 와 는 점성 선속 벡터(viscous flux vector), 는 소스 벡터(source vector)를 의미하며, , 𝛤 은 자코비안 행렬, 예조건화 행렬이다.
MUSCL(Monotonic Upstream-centered Scheme for Conservation Laws)기법[16]을 사용하여 대류항을 이산화하였으며, 물리적 시간에 대해 2차 후방 차분법을, 의사시간에 대해 1차 후방 차분법을 사용하였다[12].
마이크로 버블의 붕괴는 응축, 증발과 같은 상변화 과정에 의해 영향을 받는다. 포화증기압과 국소압력의 크기 차이에 따라 질량전달량이 결정되고 그 강도는 ,에 의해 조절된다[17,18].
물리적 시간의 전진(physical time stepping) 중에는 고차 정확도의 상경계 포착기법을 완전 압축성 모델과 결합하여 정확도를 높일 수 있었다. 질량 이동을 고려한 기체상의 계산 영역 내 상경계 이류 방정식은 다음과 같다.
고차 정확도 상경계면 포착기법은 체적분율에 대한 이류방정식을 매 물리적 시간마다 추가적으로 계산하여 더욱 정확한 상경계면을 도출할 수 있다. 물리적 시간에대해 2차 정확도 후진차분법, 대류항에 대해 압축성 상류차분법(compressible upwind scheme)을 사용한다. 이산화된 이류 방정식은 다음과 같다.
이상의 수치해석 방법과 캐비테이션 모델에 대한 자세한 추가적인 설명은 참고문헌[9,10,11,12,13,14,15,16,17]을 참고하기 바란다.
3. 수치해석 결과
HIFU에 의해 형성된 벽면 주변에서의 버블역학에 대한 연구가 Daniel J. Laser 등[5]에 의해 실험, 수치해석으로 수행되었다. 해당 연구에서 관측된 벽면 주변에서 형성되는 벽면에 의해 잘린 타원형 구체 마이크로버블은 Fig. 1과 같은 형상을 가진다. 여기서 이격거리 은 버블 중심으로부터 벽면까지 수직거리이며, 과는 각각 버블 중심으로부터 경계면까지 수평거리, 수직거리를 의미한다. 벽면과 버블 사이는 무차원 이격거리로 표현할 수 있으며 그 정의는 다음과 같다.
벽면 중심에서 최고 압력이 나타나는 시간 에 의해 무차원화된 시간 은 다음과 같이 정의된다.
본 연구에서는 각기 다른 4가지 무차원 이격거리에 대한 버블의 붕괴에 대한 분석을 수행하였다.
3.1 해석 대상 및 경계조건
본 연구에서는 해석시간의 단축을 위해 벽면에 부착되어 발생하는 버블 중심축 기준으로 좌우 대칭이라고 가정하여, 축대칭 모델을 사용하였다. 매끄럽고 평평한 벽면으로 가정하여 실제 벽 주변에서 발생할 수 있는 불규칙한 압력파의 반사를 고려하지 않았다.
Table 1은 해석 영역 내의 액상 및 기상(버블)의 초기 온도, 압력, 밀도를 나타낸다. 또한, 액상 내부에 Fig. 1과 같은 형태를 가지는 버블의 최대 성장시 축방향 및 수직방향 버블 초기 반지름 , 는 각각 31 , 20 이다. 각 초기조건은 실험 결과를 바탕으로 도출되었다[5]. 액상의 초기 압력의 경우 버블이 최대 크기까지 성장한 후 붕괴하는 동안의 시간(0 𝜇s<t<0.9 𝜇s)에 따른 평균 압력으로 가정하였다. 실험에서 해당 시간 동안의 초음파의 진폭에 의해 버블 생성 영역은 1.4±0.4Mpa의 압력 진폭을 가진다. 벽면에서의 입사파와 산란파의 간섭으로 인해 진폭이 약 50%까지 증가하였고, 이로 인한 버블의 붕괴시간 동안 1.55 의 시간에 대한 압력 평균값이 도출되었다. 전산해석영역은 HIFU 생성 음향기기에 의해 초음파가 집중되는 영역(3×6 cm)에 비해 상대적으로 작기 때문에, 버블과 멀리 떨어진 영역에서의 압력은 일정하다고 가정하였다[5].
Table 1.
Property of fluid
| Liquid | Gas(bubble) | |
| Temperature(K) | 296 | 296 |
| Pressure(Mpa) | 1.55 | 0.101 |
| Density(kg/m3) | 1000 | 1.2 |
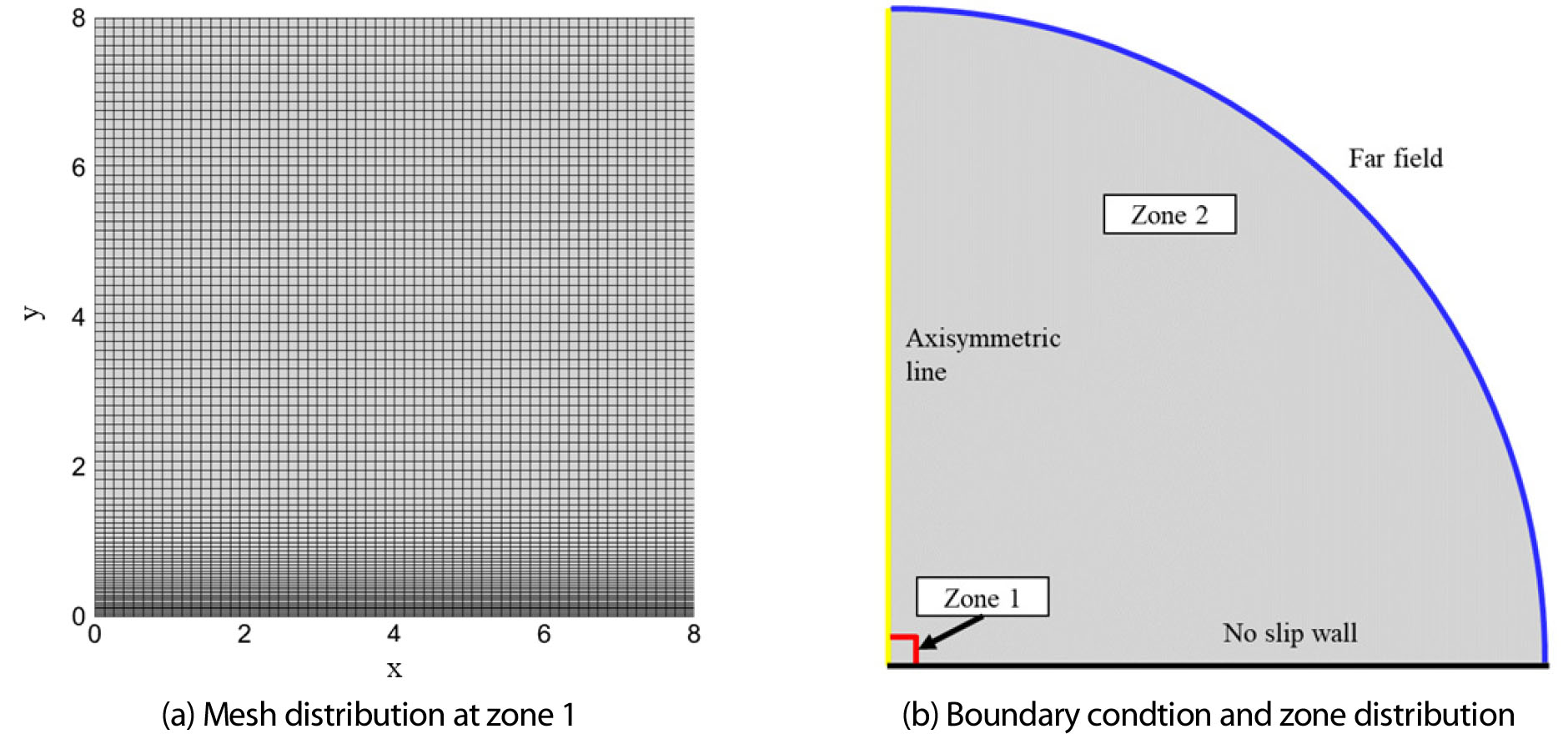
Fig. 2(a)는 전산해석영역과 경계조건을 보여준다. 효과적인 격자 형성을 위해 버블의 거동이 주로 이루어지는 영역(Zone 1)에서의 격자를 더욱 조밀하게 구성하였고 그 외의 영역(Zone 2)로 나누어 해석영역을 형성하였다. 버블로부터 멀리 떨어진 외부 경계에는 far field condition이 적용되었으며, 벽면에는 점착조건(no-slip condition)을 적용하였다. Fig. 2(b)과 같이 벽면에서의 충격파, 버블 거동 변화, 온도의 정확한 포착을 위해 조밀한 격자를 생성하였다.
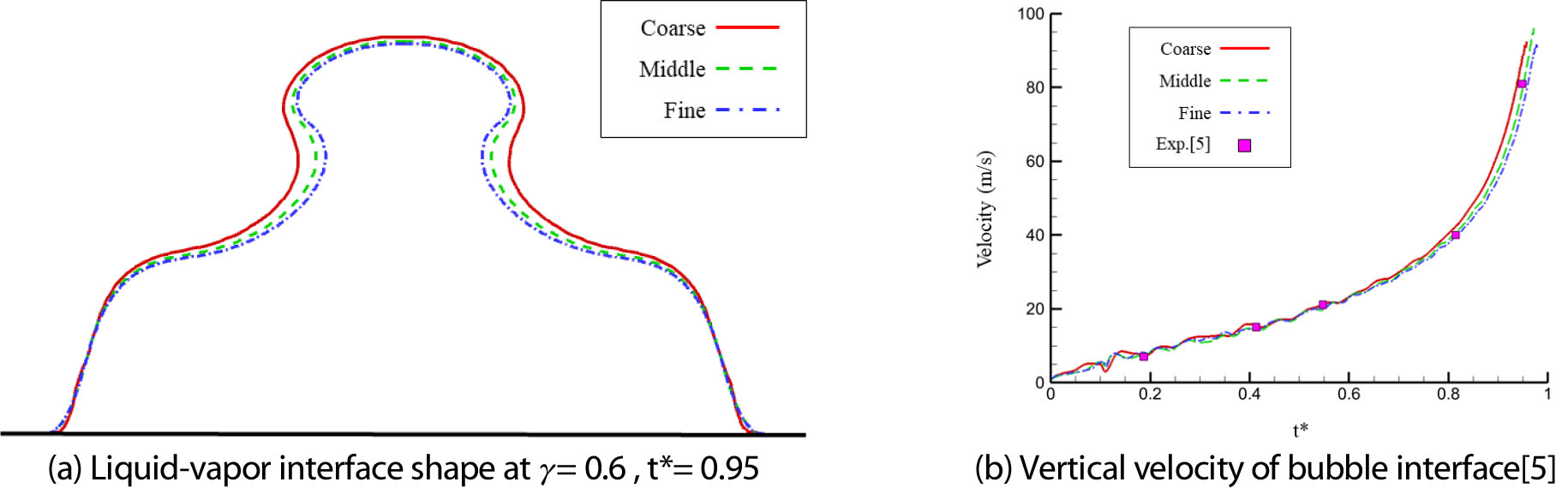
Zone 2에서 각각 다른 격자수를 가지는 성긴격자(100×100), 중간격자(200×200), 조밀격자(300×300)인 경우에 대하여 해석결과를 비교하였다. Fig. 3의 (a)는 무차원 이격거리 0.6의 무차원 시간 0.95에서의 형상을 나타낸다. 격자가 조밀해짐에 따라 목이 얇아지는 것을 확인할 수 있다. 가장 적은 수의 격자를 가지는 경우와 다른 두 격자의 경우 버블 목을 형성하며 목의 크기의 차이가 분명하게 나타난다. Fig. 3의 (b)는 각 격자 조건에서의 버블 경계면의 수직 속도를 나타낸다. 중간격자와 조밀격자의 경우 버블붕괴 과정에서 서로 형상 및 수직 붕괴 속도의 차이가 적음을 알 수 있다. 본 연구에서는 해석결과의 일관성과 해석속도의 이점을 위해 모든 해석에 대하여 중간격자를 사용하였다.
3.2 수치해석 검증
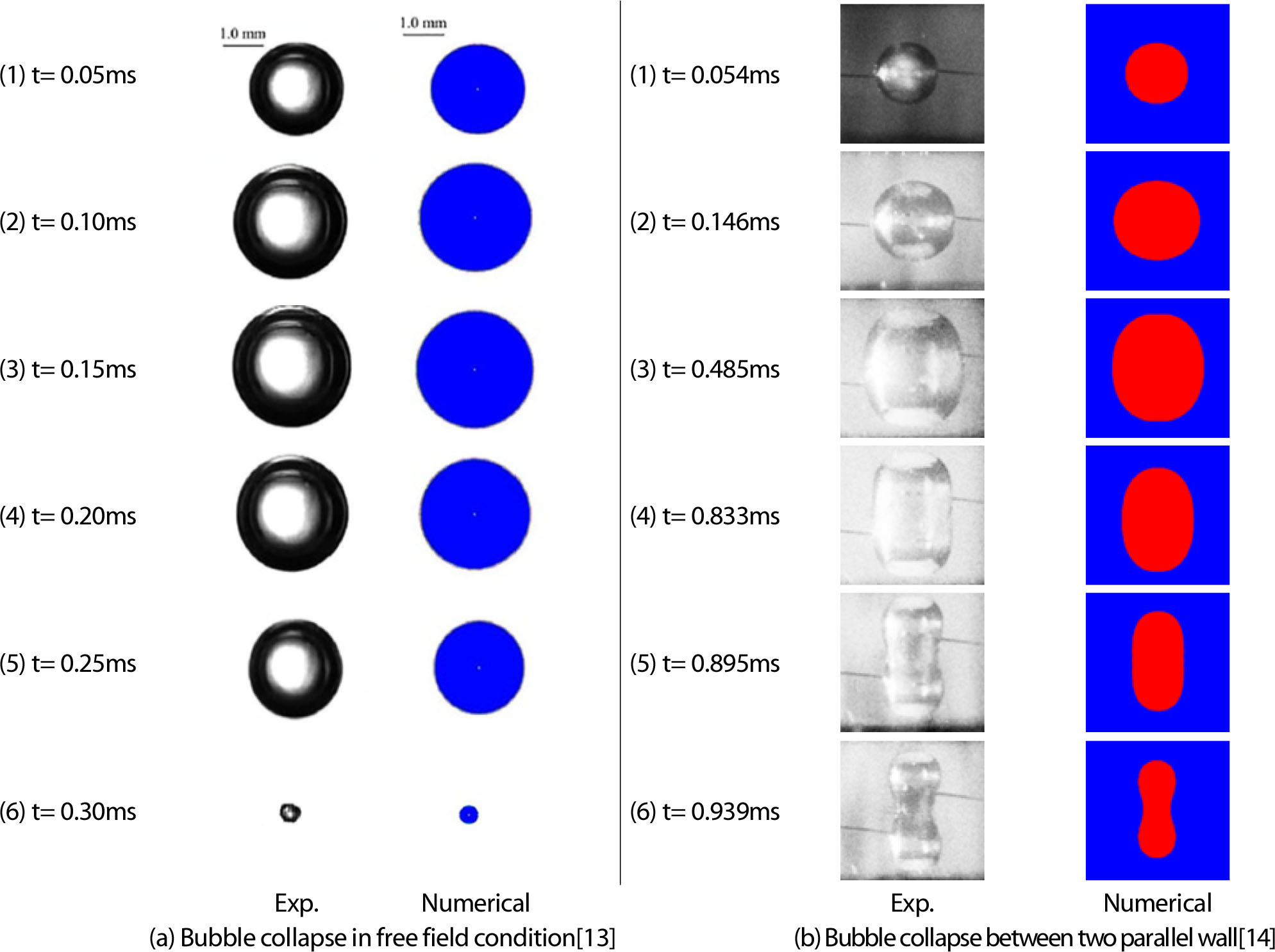
Fig. 4는 자체개발 코드의 각각 다른 두 조건에서의 결과와 실험 결과의 비교 결과들이다. Fig. 4의 (a)는 20°의 외기온도를 가지는 대기압에서 14.6 mJ의 레이저 에너지를 사용하여 생성된 마이크로버블의 1차 붕괴까지 한 주기의 버블 붕괴에 대한 실험과 해석의 비교 결과이다[13]. Fig. 4의 (b)는 평행한 두 평판 사이에서 0.23 Mpa, 298 K의 초기값을 가지는 액상 중심에서 2 mm의 반지름과 4.53 Mpa, 1200 K의 초기 압력, 온도를 초기조건으로 하는 버블의 해석결과와 실험결과의 비교 결과이다[14].
3.3 무차원 이격거리(𝛾)에 따른 버블붕괴 분석
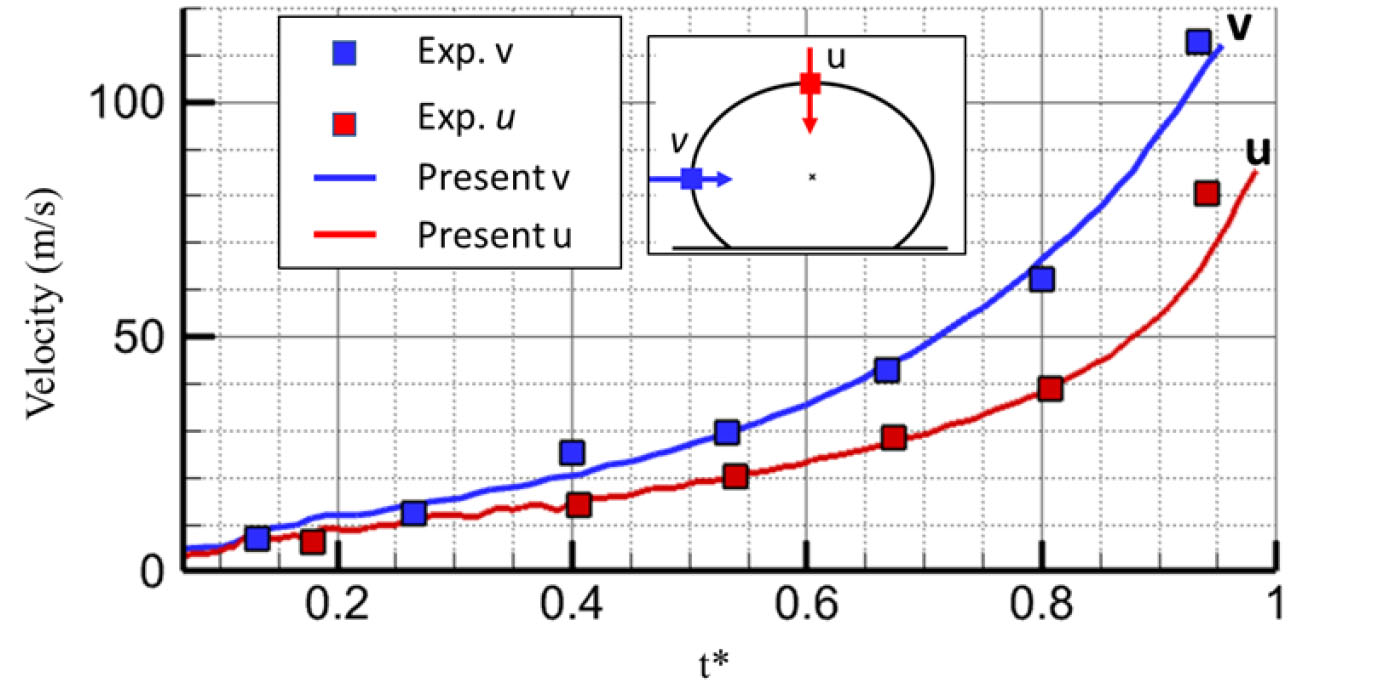
Fig. 5는 무차원화된 시간()에 따른 버블 경계면의 벽과 수평한 속도(v)와 수직한 속도(u)의 전산해석 결과와 실험치의 비교이다. 벽면에 부착된 타원형 버블의 붕괴 과정에서 벽면에 의한 유동의 제한 때문에 버블 경계면이 벽과 수직한 방향으로 붕괴하는 속도보다 벽과 수평한 방향으로 붕괴하는 속도가 빠르게 나타난다. 𝛾=0.4의 이격거리를 가지는 버블 붕괴 해석결과 두 속도 모두 실험치와 비슷한 결과를 나타낸다. 두 속도 성부 모두 실험결과와 잘 일치함을 보였다. 붕괴 속도 차이로 인해 상반구 옆면에서 버블 중심 반경으로 말려 들어가며 붕괴가 진행되며 중심부가 극단적으로 얇아져 상단과 하단의 두 버블 영역으로 나누어진다. Fig. 6의 (a), (b)는 각각 Daniel J. Laser등[5]의 실험결과와 전산해석결과이며, (c)는 본 연구에서 사용한 전산해석 코드의 𝛾=0.4인 경우 액상 체적분율(Liquid volume fraction) 0.5 기준으로 양분하여 버블 형상을 나탄내다. 버블 붕괴 형상 또한 실험결과와 다른 전산해석 모델의 결과와 비슷한 결과를 보임을 알 수 있다.
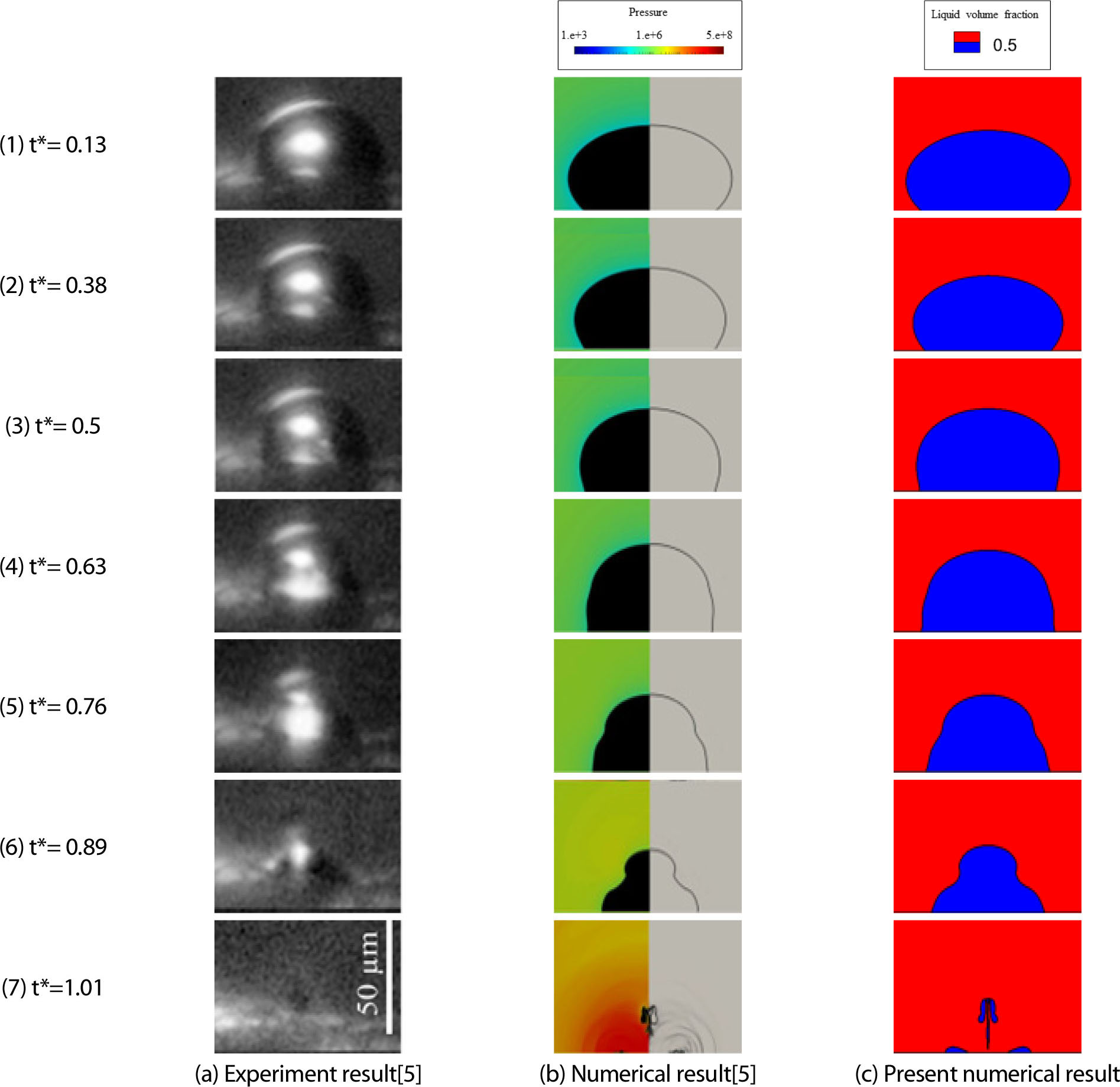
Fig. 6.
Comparison of experimental and numerical result of Daniel J. Laser[5] with present numerical result
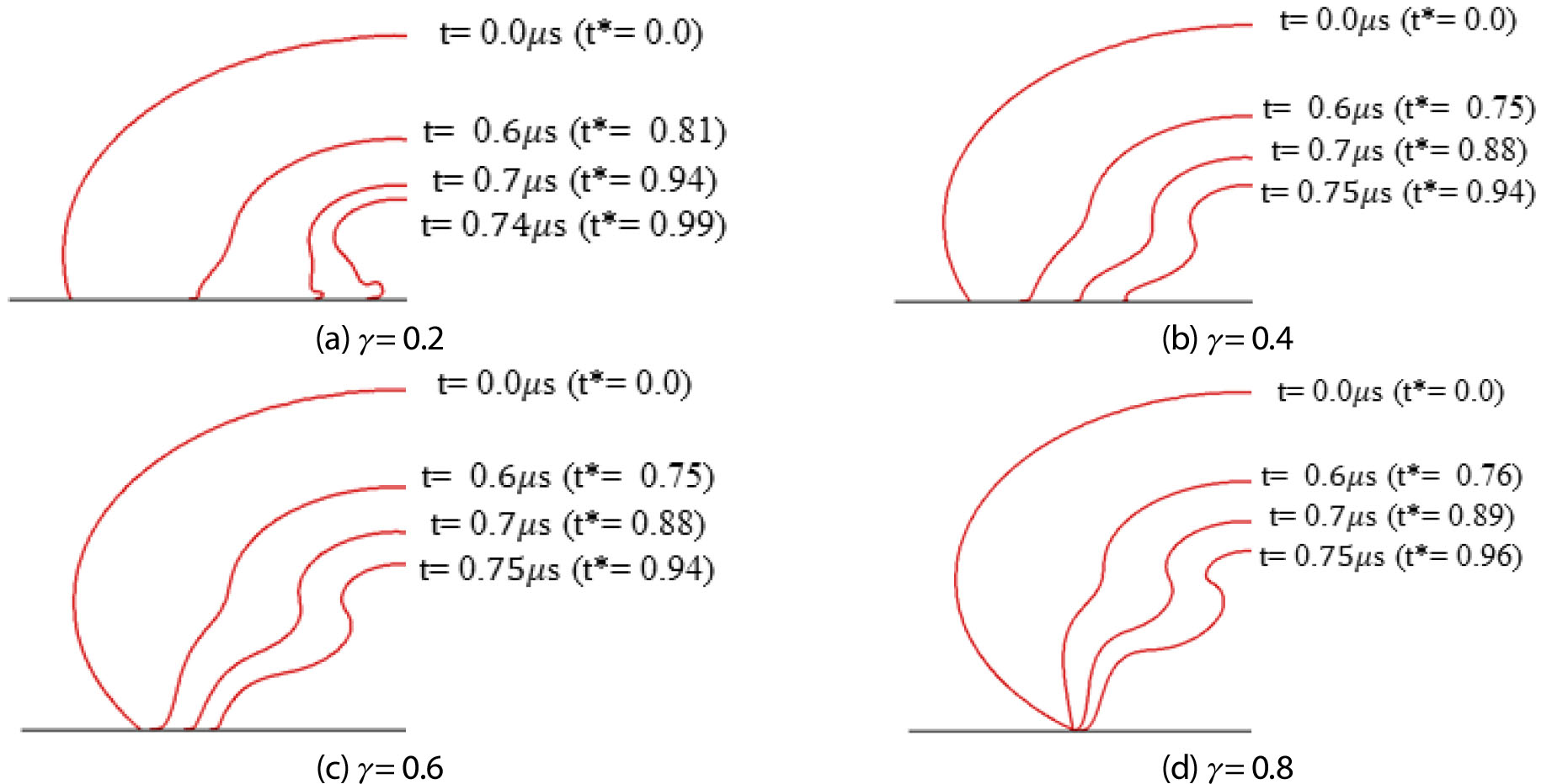
Fig. 7의 경우 각각의 무차원 이격거리에 따른 마이크로 버블의 제트 형성 전까지의 붕괴과정 동안의 버블 형상을 나타낸다. 이격거리가 작을수록 버블 중심과 벽면과 부착된 경계면의 거리가 멀기 때문에 벽면에서의 버블 붕괴 속도가 상대적으로 빠르게 나타난다. 𝛾=0.2의 경우 벽면에서의 버블 경계면의 붕괴 속도가 빠르게 형성되어 벽면과 부착된 영역의 크기가 빠르게 줄어들지만 𝛾=0.8의 경우 중심과 가장 멀리 떨어진 경계면이 벽면과도 상대적으로 멀리 떨어져 있어 벽면과 부착된 경계면의 붕괴가 거의 나타나지 않는 것을 확인할 수 있다. 이러한 붕괴 특성에 의해 이격거리가 증가함에 따라 하부 영역의 크기 또한 증가한다. 𝛾=0.4, 0.6, 0.8의 경우 축 방향 수축에 의해 버블의 중심축에서 벽면과 비교적 먼 거리에서 얇은 목을 형성한다. 𝛾=0.2의 경우 비교적 벽면과 가까운 거리에서의 축 방향 수축이 일어나고 중심축에서 벽면과 비교적 가까운 거리에서 목을 형성한다.
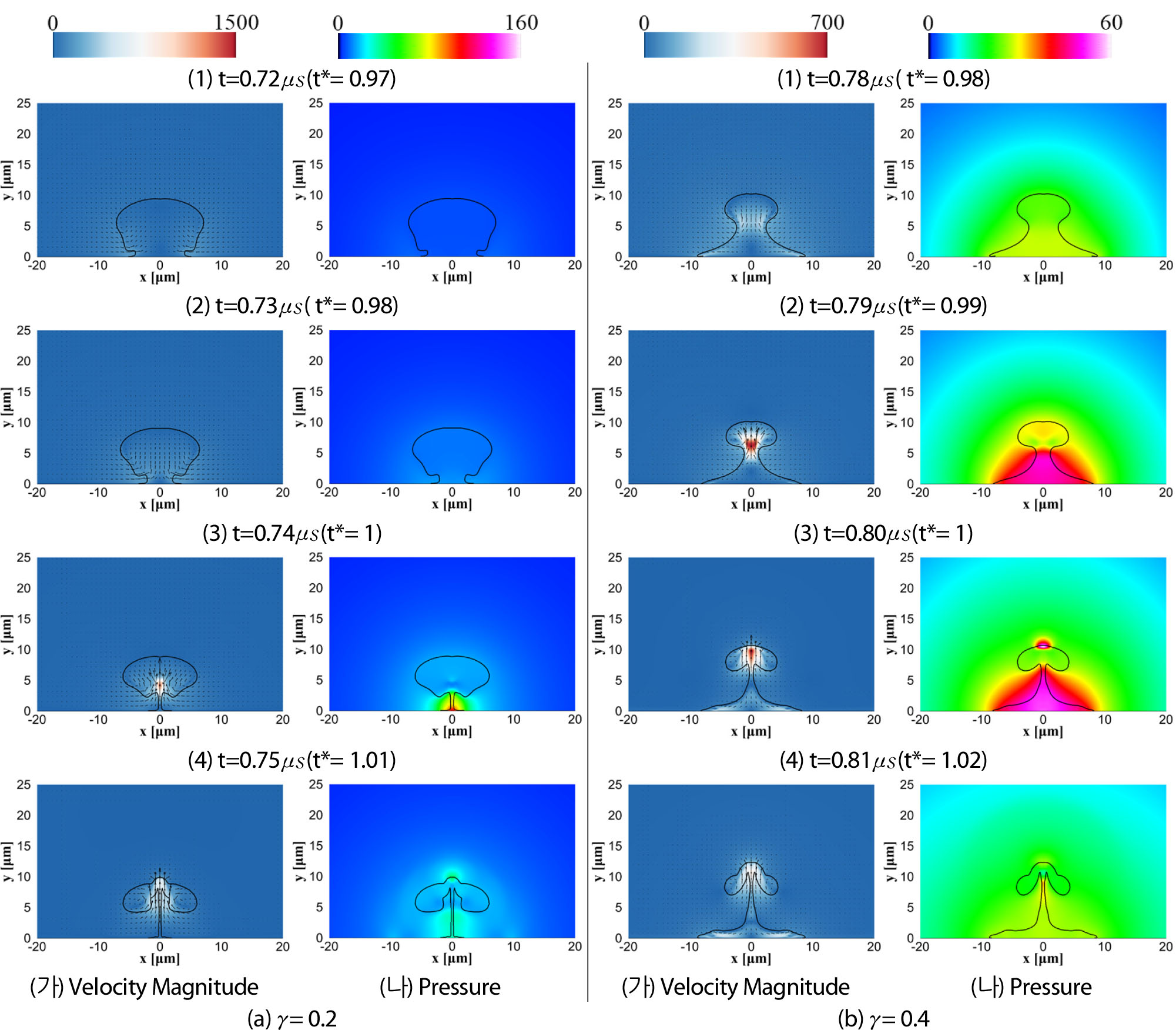
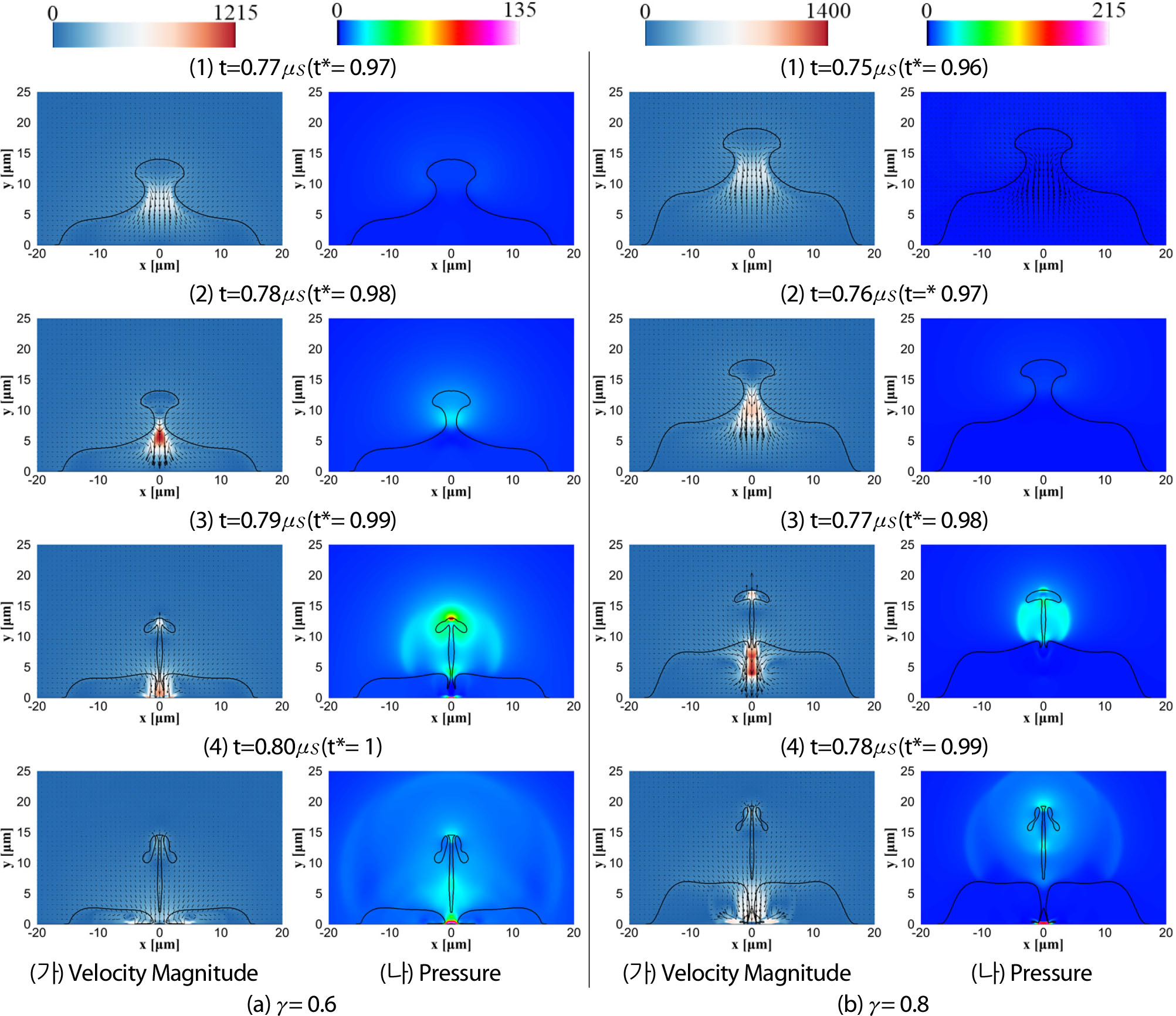
Fig. 8과 9는 각각의 이격거리에 대한 마이크로 제트 형성 과정 중 상경계면, 속도장(가) 및 압력장(나) 결과를 나타낸다. 벽면과 버블의 중심이 가장 가까운 𝛾= 0.2의 경우 벽면에 부착된 버블의 압축에 의한 직접적인 압력상승 효과가 벽면에 발생한다. 반면 마이크로 제트는 벽면의 반대 방향으로 형성되어 충격력이 벽면에 전달되지 못한다. 𝛾=0.4의 경우 벽면에서의 버블 압축으로 인한 압력상승이 상대적으로 낮게 나타나며, 마이크로 제트 또한 벽면 반대 방향으로 형성된다. 𝛾=0.6, 0.8의 경우 버블의 상부 영역에서는 벽면과 반대 방향, 하부에서는 벽면 방향으로 각각 마이크로 제트가 발생하며 벽면에서는 버블 하부 영역의 수축에 의한 압력상승과 마이크로 제트의 직접적인 충격력이 벽면 중심부 압력 증가의 주요한 인자로 작용한다.
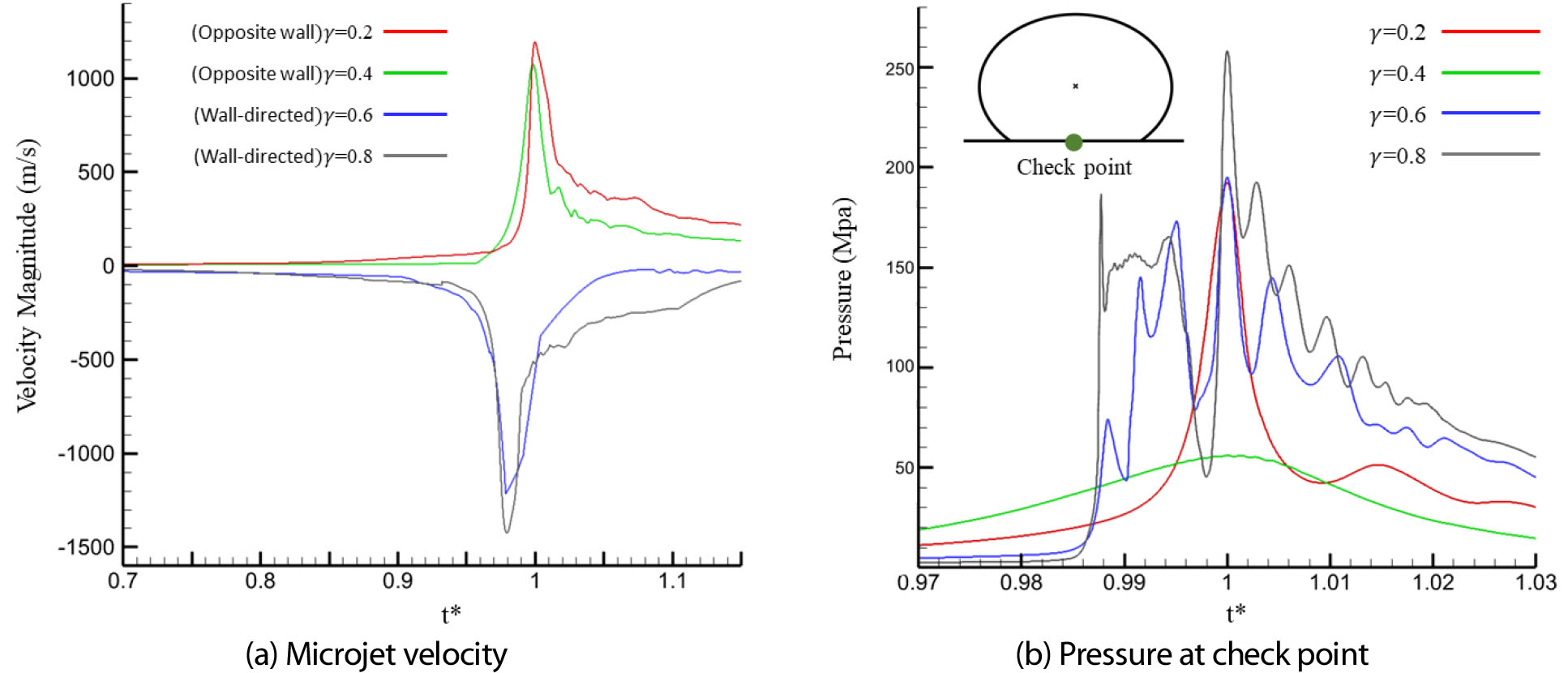
Fig. 10(a)는 각 무차원 이격거리 별 시간에 따른 마이크로 제트의 속도 결과이다. 𝛾=0.2, 0.4의 경우 마이크로 제트는 벽면과 반대 방향으로 형성되며 𝛾=0.6, 0.8의 경우 마이크로 제트가 벽면을 향하여 속도를 가짐을 확인할 수 있다. 𝛾=0.8의 경우 하부 영역 제트가 상대적으로 길게 형성되며 충분히 발달할 수 있는 공간을 갖기 때문에 가장 빠른 최대속도 1425 m/s를 가진다. 𝛾=0.6의 경우 제트가 형성되기 시작하는 영역과 벽면 사이의 거리가 상대적으로 짧아 충분히 발달하지 못하고 벽면과 부딪히기 때문에 보다 낮은 1214 m/s의 속도를 가지는 제트가 형성된다.
Fig. 10(b)은 무차원 이격거리 별 시간에 따른 벽면 중심에서의 압력 결과이다. 벽면의 압력상승은 마이크로 제트의 직접적인 충격과 버블의 압축 그리고 1차 붕괴후 형성되는 작은 버블들의 연쇄적인 팽창, 압축 붕괴에 의해 나타난다. 이러한 요인들로 인해 벽면 중심에서 최대 압력이 나타나는 =1 전후로도 여러 번의 압력상승이 일어난다. =1 이전의 압력 상승은 벽면과 부착된 버블의 압축에 의한 압력상승의 결과이다. =1이후의 압력상승은 버블의 1차 붕괴 이후에 여러개의 작은 버블로 나누어지고 연쇄적으로 붕괴할 때 발생하는 압력파의 영향으로 인한 압력상승이다. 𝛾=0.2, 0.4의 경우 마이크로 제트에 의한 압력상승은 발생하지 않으며, 1차 붕괴에서의 버블 압축에 의한 압력상승이 가장 큰 압력 상승으로 나타난다. 𝛾=0.4의 경우 버블 연쇄 붕괴가 상대적으로 벽면과 멀리 떨어진 영역에서 느리게 발생하기 때문에 연쇄 붕괴에 의한 압력 상승이 나타나지 않는다. 𝛾=0.6, 0.8의 경우 버블 압축에 의한 압력상승, 마이크로 제트의 직접적인 충격에 의한 압력상승, 작은 버블들의 연쇄적인 팽창, 압축, 붕괴에 의한 압력상승 모두 나타나는 것을 알 수 있다. 마이크로 제트가 충분히 발달하여 벽면을 충격하는 𝛾=0.8의 경우 벽면 중심에서 관측된 최고 압력은 모든 조건 중에서 가장 높은 약 257 MPa로 나타났다. 𝛾=0.4의 경우 벽면에서의 버블 압축에 의한 압력상승이 낮을 뿐만 아니라 마이크로 제트 또한 벽면의 반대 방향을 향하기 때문에 벽면 중심에서의 최고 압력이 56 Mpa로 가장 낮은 것을 확인할 수 있다.
4. 결 론
본 연구에서는 선행연구를 바탕으로 HIFU에 의해 형성되는 벽면에 부착된 타원형 구체 버블의 무차원 이격거리에 따른 붕괴특성을 압축성 축대칭 Navier-Stokes 방정식 기반의 균일 혼상류모델을 사용하여 수치해석을 통해 분석하였다. 계산 시간을 단축하기 위해 복잡한 현상을 단순화하여 타원형 버블의 붕괴 과정에 집중함으로써, 마이크로버블 역학을 보다 효과적으로 모델링하고 예측할 수 있었다. 선행연구의 실험 결과와 버블의 상경계면 형상 및 축 방향, 벽 방향 상경계 이동속도를 비교하여 결과가 잘 일치함을 보여 자체개발 코드의 정확도를 검증할 수 있었다. 무차원 이격거리의 변화에 따라 버블붕괴 특성, 속도장, 압력장을 분석하고 버블 붕괴시 발생하는 버블의 압축과 마이크로제트에 의한 벽면의 압력상승의 영향을 고찰하였다.
본 연구의 내용을 요약하면 다음과 같다. 자체 개발 수치해석 코드를 사용하여 타원형 구체 버블의 붕괴 과정을 모사하여 실험치와 잘 일치함을 보였다, 이격거리에 따라 벽면과 부착된 버블 경계면의 붕괴 속도가 다르게 나타났다. 이격거리가 가까울수록 벽면에서의 버블 수축 속도가 빠르게 나타났으며 이격거리가 멀어질수록 그 속도는 줄어들었다. 마이크로 제트의 형성 특성에 따라 벽면에 미치는 특성이 다르게 나타남을 확인하였다. 이격거리가 멀어짐에 따라 벽면을 향하는 마이크로 제트의 발달이 충분히 이루어졌다. 무차원 이격거리 0.2의 경우 마이크로 제트의 속도는 약 1193 m/s로 빠르게 형성되지만 벽면 반대 방향을 향하며 벽면에서의 압력상승은 벽면과 부착된 버블의 압축에 의해서만 나타났다. 무차원 이격거리 0.4의 경우 벽면에서의 압력상승이 가장 적게 나타났다. 마이크로 제트의 방향이 벽면 반대방향을 향할 뿐만 아니라 벽면에서의 버블 압축에 의한 압력상승 효과도 미미하게 나타났다. 무차원 이격거리 0.6, 0.8의 경우 벽면에서의 버블 압축 뿐만 아니라 벽면을 향하는 마이크로 제트의 충격력에 의한 압력 상승이 발생하였다. 0.6의 경우보다 0.8의 경우 마이크로 제트가 충분히 발달할 공간의 여유를 갖기 때문에 그 속도가 약 1425 m/s로 더 높은 것을 확인할 수 있다.