1. 서 론
2. 전산해석 기법 및 격자
2.1 LBM 전산해석 기법
2.2 NASA WIPP 모델
2.3 전산해석 격자 및 유동 조건
3. 전산해석 결과
3.1 상호작용이 날개 공력 특성에 미치는 영향
3.2 상호작용이 날개 주변 유동장에 미치는 영향
3.3 상호작용이 프로펠러 공력 특성에 미치는 영향
3.4 상호작용이 프로펠러 후류 구조에 미치는 영향
4. 결 론
1. 서 론
대기 오염, 온실가스 배출 증가, 기후 온난화가 빠르게 진행됨에 따라 탄소 중립 달성을 위한 전 지구적인 노력이 이루어지고 있다. 항공기 산업은 전체 탄소 배출량의 약 2~3% 수준을 차지하고 있으나, 2010년 이후 항공 승객의 수가 많아짐에 따라 탄소 배출량이 지속적으로 증가하고 있어 항공 부문에서도 탄소 배출량 저감이 시급하다[1]. 탄소 배출량 저감을 위해 기존의 항공유 기반의 동력원을 대신하여 태양광 에너지, 연료전지, 배터리 등의 동력원을 이용하는 친환경 항공기에 대한 개발 수요가 꾸준히 증가하고 있다. 그 중 연료전지는 가장 실용적인 대안으로 주목받고 있으며[2], 날개에 여러 개의 프로펠러를 사용하는 분산전기추진(Distributed Electric Propulsion, DEP) 시스템과 같은 적용하는 사례가 많이 보고되고 있다[3]. 분산전기추진 시스템은 소수의 대형 추진장치를 다수의 소형 추진장치로 나누어 기체에 분산 배치하는 방식으로, 추진시스템의 Redundancy를 확보할 수 있을 뿐만 아니라 다중 모터 및 제어기 구성을 통해 추진시스템을 이중화하여 제어력과 조종성을 향상시킬 수 있다[4]. 또한 여러 개의 프로펠러에 의해 가속된 유동을 활용하면 날개 표면에서의 유동 박리 지연 효과가 있고 고양력을 생성할 수 있다[5]. 이러한 장점으로 인해 분산전기추진 시스템을 적용한 Multirotor, Vectored Thrust, Lift+Cruise와 같은 형태의 미래형 비행체 개발 연구가 활발하게 진행되고 있다[6,7,8,9]. 하지만 프로펠러의 개수가 증가함에 따라 프로펠러-날개 간의 간섭현상은 더욱 빈번하게 발생한다. 프로펠러의 후류가 발달하는 방향으로 날개와 같은 구조물이 존재하는 경우, 프로펠러의 나선형 후류 구조 발달이 방해 받고 국부적으로는 지면 효과가 발생한다[10]. 또한, 프로펠러-날개 간의 간섭현상으로 인해 발생하는 비정상 공력 하중은 비행체의 진동 유발하고 소음 수준을 증가시킨다[11]. 따라서 고효율/저소음의 분산전기추진 비행체를 설계하기 위해서는 프로펠러-날개 상호작용으로 인한 공기역학적 간섭 효과를 보다 정확하게 예측하고 분석할 필요가 있다.
프로펠러-날개 간의 공기역학적 상호작용 효과를 분석하기 위한 선행 연구는 시험 또는 전산해석적 접근을 통해 수행되었다. Witkowski 등[12]은 풍동실험과 와류 격자법을 적용한 전산해석을 수행하여 프로펠러의 전진비 증가 및 날개의 종횡비 감소에 따라 날개의 양항비가 감소하는 경향성을 확인하였다. Rangwalla 등[13]은 프로펠러에서 발생하는 후류가 날개 주변 순환 분포에 미치는 영향을 분석하였다. 특히 프로펠러의 올림흐름 효과를 받는 날개의 경우, 내림흐림 효과를 받는 날개보다 순환 강도가 증가함을 확인하였다. Tai 등[14]은 프로펠러 효과가 반영 가능한 패널 기반의 공력해석 기법을 개발하였다. 프로펠러 후류의 올림흐름과 내림흐름 효과가 회전 방향에 따라 발생하는 공력해석에 대한 검증을 진행하였으며 KARI의 OPPAV(Optional Piloted PAV) 비행체 해석에 적용하여 결과 분석을 진행하였다. Chandukrishna 등[15]은 날개 끝단 프로펠러를 Tractor, Pusher 타입으로 구분한 후 날개에 미치는 공기역학적 영향성을 비교 분석하였다. Tractor 타입의 경우 날개가 후류의 영향을 직접적으로 받아 Pusher 타입보다 날개의 공력성능이 더 우수하게 나타남을 확인하였다. Park 등[16]은 날개의 고양력 장치 장착 여부에 따라 프로펠러 후류 및 공력 성능에 미치는 영향을 분석하였다. 고양력 장치를 장착한 날개의 경우, 프로펠러 후류에 의해 최대 양력 계수가 증가하였으나 실속이 발생하는 받음각이 작아지는 현상을 유발하였다. 날개의 공력 특성 변화 또한 프로펠러 장착 위치에 따라 지배적인 영향을 받는 사실을 과거 연구로부터 확인하였다. Choi 등[17]은 프로펠러와 날개 사이의 상대거리 변화에 따른 날개의 공력 변화를 분석하였다. 프로펠러는 날개 끝에 가까워질수록 날개의 단면 양력 계수 분포에 미치는 영향이 감소함을 확인하였다. Kim 등[18]은 Quad-Tilt Propeller 형상의 무인기 날개에서 발생하는 공력 현상에 대한 실험을 진행하였다. 풍동실험을 통해 전방 날개의 프로펠러로 인한 후방날개의 굽힘 모멘트, 속도 변화를 분석하였으며, 전방 날개의 프로펠러는 후방날개에 큰 영향을 주지 않은 것을 확인하였다. Catalano 등[19]은 Pusher 프로펠러의 장착 위치에 따른 날개의 양항비를 비교 분석하였다. 프로펠러-날개 간 수직거리를 변화했을 경우, Low Position보다 High Position일 때 더 높은 양항비가 나타남을 확인하였다. Aref 등[20]은 프로펠러의 회전 방향, 위치에 따른 날개의 양력계수를 비교하였다. 날개 기준 Inboard 위치에서 프로펠러를 Counter Clock Wise(CCW) 방향으로 회전할 경우 날개의 양력계수가 우수하게 나타났다.
선행 연구 조사 결과와 같이 프로펠러-날개 간의 상호작용은 공기역학적 성능 면에서 중요한 요소로 작용한다. 특히 날개 끝에서 발생하는 와류를 감소시키며 양력 증가를 유발하는 날개 끝단 부착 프로펠러는 효율적인 측면으로도 많은 이점을 가지고 있다. 따라서 본 연구에서는 날개 끝단 부착 프로펠러 모델을 적용하여 날개 받음각 변화에 따른 프로펠러-날개 간의 상호작용을 분석하였다. 본 연구의 목적은 여러 개의 프로펠러가 장착된 분산전기추진 시스템 전산해석 연구의 사전 연구로, 날개 끝 Tractor 프로펠러로 구성된 NASA의 Workshop for Integrated Propeller Prediction(WIPP) 모델을 이용하여 프로펠러-날개 상호 공력간섭 현상의 물리적인 특성을 분석하고 해석자의 검증을 수행하는 것이다. Lattice-Boltzmann Method(LBM) 기반의 상용 소프트웨어인 PowerFLOW를 통해 전산해석을 수행하였으며, NASA의 실험 데이터를 활용하여 해석자의 정확성 검증을 진행하였다. 또한 날개 끝 프로펠러가 날개에 미치는 영향을 분석하기 위해 날개의 표면 압력 분포, 후류 구조, 양력, 항력 성능을 비교하였다.
2. 전산해석 기법 및 격자
2.1 LBM 전산해석 기법
대부분의 선행 연구에서 Reynolds Averaged Navier-Stokes(RANS) 지배방정식을 사용하는 전산유체역학(Computational Fluid Dynamics, CFD) 해석을 통해 결과를 분석하였다. Navier-Stokes 방정식은 유동의 점성으로 인한 영향과 압축성 효과를 고려할 수 있어 정확한 해석 결과를 도출할 수 있지만 많은 격자 수와 반복적인 계산으로 인한 해석 시간이 오래 걸리는 단점이 존재한다[21]. 따라서 최근에는 입자 밀도 분포에 대한 Boltzmann 방정식 기반의 LBM 전산해석 기법을 사용하여 공력 성능을 예측하는 연구가 다수 진행되고 있다[22,23,24]. LBM 전산해석 기법은 지배방정식이 대수방정식 형태이고 효율적인 병렬화 구조로 인해 기존 CFD에 비해 해석 시간이 짧은 특징이 있다[25].
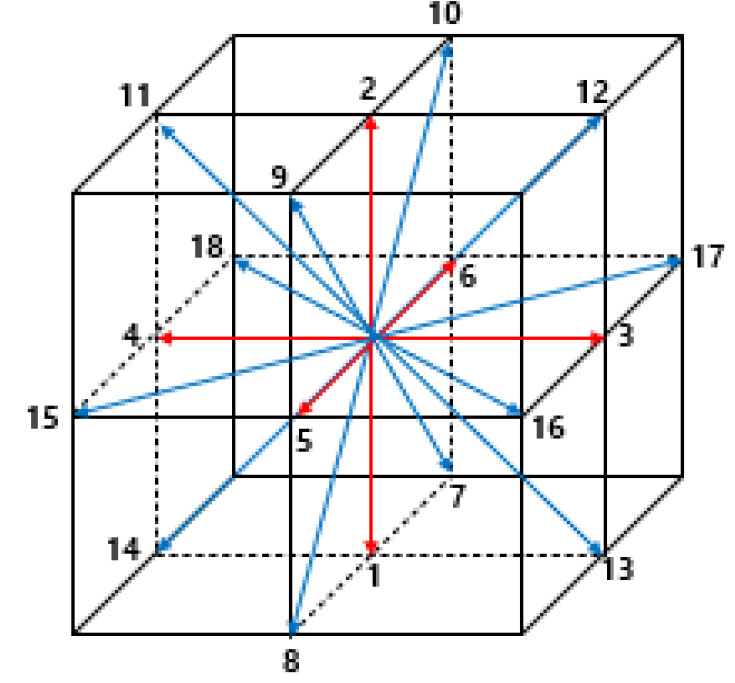
LBM 기법에서 입자들은 이산화된 격자 내에 Lattice-Boltzmann 방정식에 따라 분포되어있다. 격자 내에서 입자들은 분포함수를 따라 분포하며 지정된 방향으로 이동과 충돌이 가능하다. 입자들의 이동은 DaQb 격자 모델로 표현되며 a는 차원의 개수, b는 입자들이 이동할 수 있는 방향의 개수를 의미한다. 본 연구에서는 3차원 해석에 사용되는 D3Q19 모델을 사용하였으며, 이산화된 격자와 입자들의 이동을 Fig. 1에 표현하였다.
식 (1)은 이산화된 공간을 고려한 Lattice-Boltmann 방정식이다[26].
여기서 는 위치에서 방향으로 입자들의 위치 이동에 따른 분포함수이며 는 방향으로 이동하는 입자 속도벡터를, 는 시간의 변화를 나타낸다. 좌변의 경우 입자들의 흐름을 나타내고, 우변의 경우 입자들의 충돌을 나타낸다. 충돌 항 은 Bhatnagar-Gross-Krook(BGK) 완화 모델에 의해 다음 식 (2)와 같이 정의된다[21].
식 (2)에서의 𝜏는 완화 시간을 의미하며 입자들이 충돌한 이후 평형상태로 도달하는 시간을 무차원화로 표현한 값이다. 식 (3)는 𝜏와 동점성계수와의 관계를 식으로 나타낸 것이다.
는 Maxwell Boltzmann의 평형분포함수로 속도의 2차 항까지 Taylor 전개하여 식 (4)에 나타내었다.
여기서 는 유동 속도이며 ρ는 유체의 밀도, 는 방향으로의 가중치 상수로 식 (5)와 같이 정의된다.
격자 내에 점에서의 유체의 밀도와 운동량은 식 (1)을 이용하여 식 (6), (7)과 같이 나타낼 수 있다.
본 연구에서는 LBM-Very Large Eddy Simulation(LBM-VLES) 해석기법을 활용하여 난류 유동을 고려한 해석을 진행하였다. LBM-VLES는 Renormalization Group(RNG)의 변형된 형태를 LBM에 적용했으며, RNG k-ω 모델을 난류 점성 완화 시간을 계산하는 데 사용하였다. 식 (8)은 점성 완화 시간에 추가되는 난류 완화 시간을 나타내며, Cμ = 0.09, k는 난류 운동 에너지, 은 나선의 함수, 소용돌이, 변형을 의미한다[27].
2.2 NASA WIPP 모델
본 연구에서는 프로펠러에서 발생하는 후류와 날개 간의 공기역학적 상호작용을 연구하기 위하여 WIPP 실험 모델을 사용하였다. WIPP 모델은 40.5% 크기의 NASA X-57 항공기 날개와 날개 끝에 장착된 프로펠러로 구성되어 있다. 날개의 길이와 폭은 각각 67.07 in와 24.15 in이며, 날개 끝에는 C-130 모델 프로펠러를 10% 축소하여 지름 16.2 in 크기로 장착하였다[26]. Fig. 2는 전산해석을 수행하기 위한 WIPP 실험 모델을 나타내었다. 날개의 장착 여부에 따른 날개 주변 유동장의 변화, 프로펠러의 추력 변화, 프로펠러 후류 구조의 변화를 해석하기 위해 Fig. 2(a)와 Fig. 2(c) 모델의 해석 결과를 비교하였고, 날개 끝단 프로펠러 장착 여부가 날개의 양력, 항력, 표면 압력에 미치는 영향을 분석하기 위해 Fig. 2(b), Fig. 2(c) 모델을 사용하여 전산해석을 수행하였다.
2.3 전산해석 격자 및 유동 조건
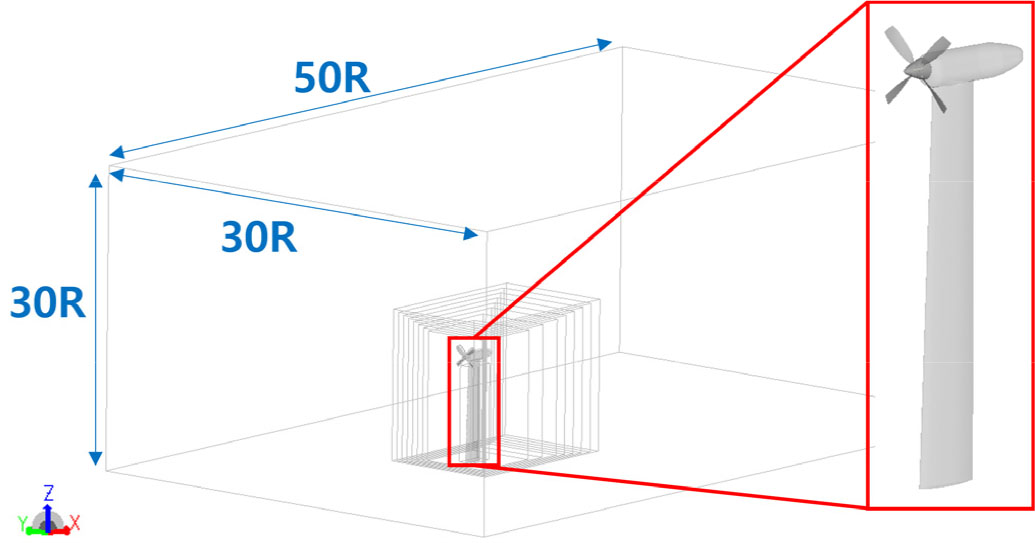
Fig. 3은 전산해석을 위한 전체 계산 영역과 조밀한 격자를 분포하기 위한 Variable Resolution(VR) 영역을 나타내었다. 전체 계산 영역의 크기는 프로펠러 반지름(R)을 사용하여 가로 길이 50R, 세로 길이 30R, 높이 30R인 직육면체로 구성하였으며 총 1억 5천만 개의 격자를 사용하였다. 격자의 조밀도 조절을 위해 전체 계산 영역을 총 15개의 VR 영역으로 구분하였고, 최소 격자의 크기는 0.3 mm으로 설정하였다. 이는 프로펠러 끝단 코드 길이의 0.3%에 해당한다. Fig. 4는 프로펠러와 날개의 공간 격자 배치를 나타내었다. 프로펠러로 인해 발생하는 후류를 효과적으로 관찰하기 위해 프로펠러 회전면을 기준으로 후류 방향에 격자를 조밀하게 배치하였다. 프로펠러 주변으로 실린더 형태의 회전 영역을 설정한 후 Sliding Mesh 기법을 사용하여 회전 효과를 부여하였다.
프로펠러 회전면을 기준으로 전면에는 Velocity Inlet 경계 조건을, 나머지 면에 Pressure Outlet 경계 조건을 부여하였다. 전산해석을 위한 유동 조건은 Table 1에 나타내었으며 NASA WIPP 실험 조건과 동일하게 구성하였다[28]. 프로펠러 회전수는 총 15회전이 되도록 하였고, 회전속도는 5,900 rpm으로 설정하였다. 수렴성을 확보하기 위해 15회전 중 10회전이 소요되었고 마지막 10회전 동안의 데이터를 시간에 대해 평균화하였다.
3. 전산해석 결과
3.1 상호작용이 날개 공력 특성에 미치는 영향
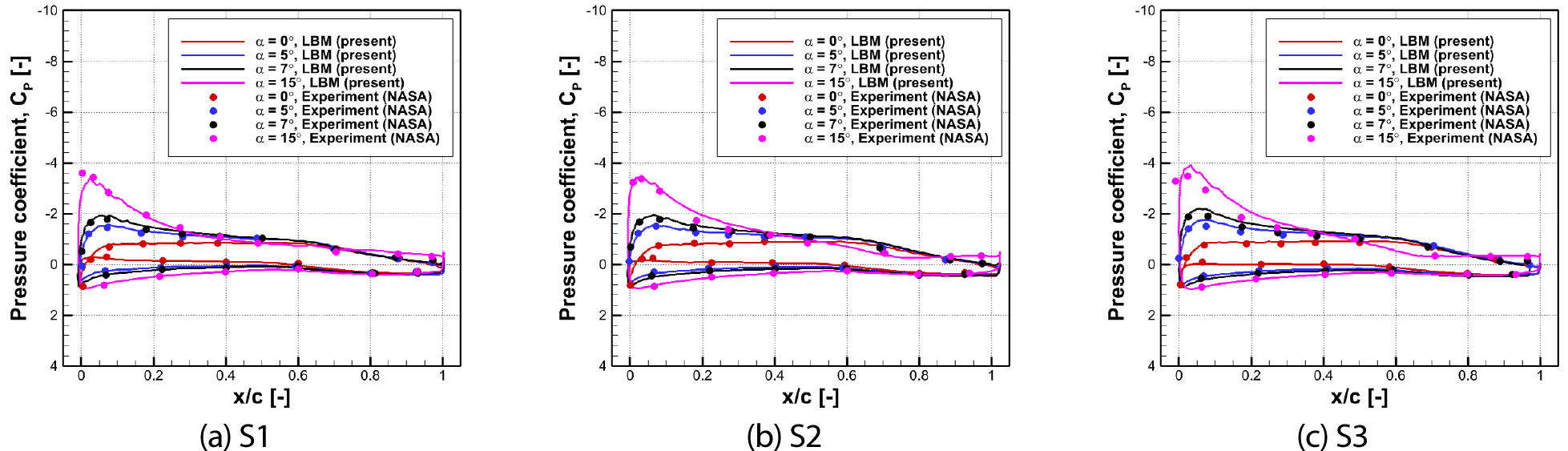
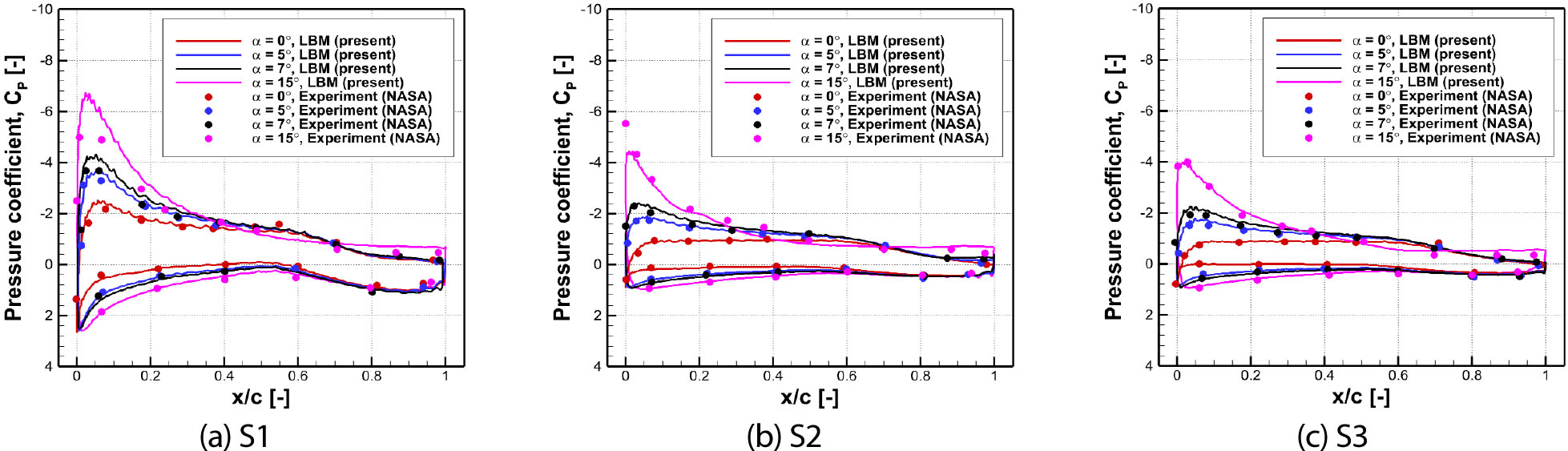
프로펠러에서 발생하는 후류 효과에 의한 날개의 양력, 항력 변화를 분석하기 앞서 연구에서 사용한 LBM 해석기법에 대한 정확성 검증을 진행하였다. Fig. 5는 NASA에서 수행한 풍동실험 결과와 비교하기 위한 Pressure Tabs의 위치를 나타내었고, 날개 스팬 길이 방향에서의 위치는 Table 2와 같다. Fig. 6과 Fig. 7에서는 해당 위치에서 프로펠러가 부착되지 않은 Unpowered Case와 프로펠러가 부착된 Powered Case의 받음각 변화에 따른 날개 표면에서의 압력계수를 실험값과 비교 및 검증하였다. 실험과 동일한 날개 받음각(α) 0°, 5°, 7°, 15° 조건에 대해 전산해석을 수행하였다. 전산해석은 총 프로펠러 회전 기준으로 15회 동안 진행하였고 마지막 10회전 동안의 결과를 평균화하여 압력계수를 비교하였다. Fig. 6과 Fig. 7을 통해 해석 결과가 전반적으로 실험 결과와 유사한 값을 도출함을 확인할 수 있었다. 다만, 날개 받음각 15° 조건에서 S1 위치(Fig. 7(a))에서는 Suction Peak의 세기를 과대 예측하였고, S2 위치(Fig. 7(b))에서는 과소 예측하는 결과가 확인되었다. 이는 동일 모델을 다른 해석자로 예측한 선행 연구 결과와도 비슷한 경향성이 보고되었다[28]. 전산해석을 통해 프로펠러가 장착되었을 때 후류 영향을 받는 위치(S1)의 압력계수는 프로펠러가 장착하지 않는 때에 비해 모든 받음각에서 Suction Peak 세기가 상대적으로 크게 해석되는 결과가 나타났다. 또한 프로펠러의 장착 여부와 상관없이 후류 영향을 받지 않는 위치(S2, S3)의 압력계수에는 큰 차이가 없음을 확인할 수 있다.
Table 2.
Tap positions for measuring the pressure and velocity
| Section | Distance from wing root(along +z direction) | Distance from spinner(along +x direction) |
| 1 | (S1) 60.995 in | (P1) 1.5 in |
| 2 | (S2) 57.386 in | (P2) 5.0 in |
| 3 | (S3) 44.386 in | (P3) 13.0 in |
| 4 | (P4) 21.0 in |
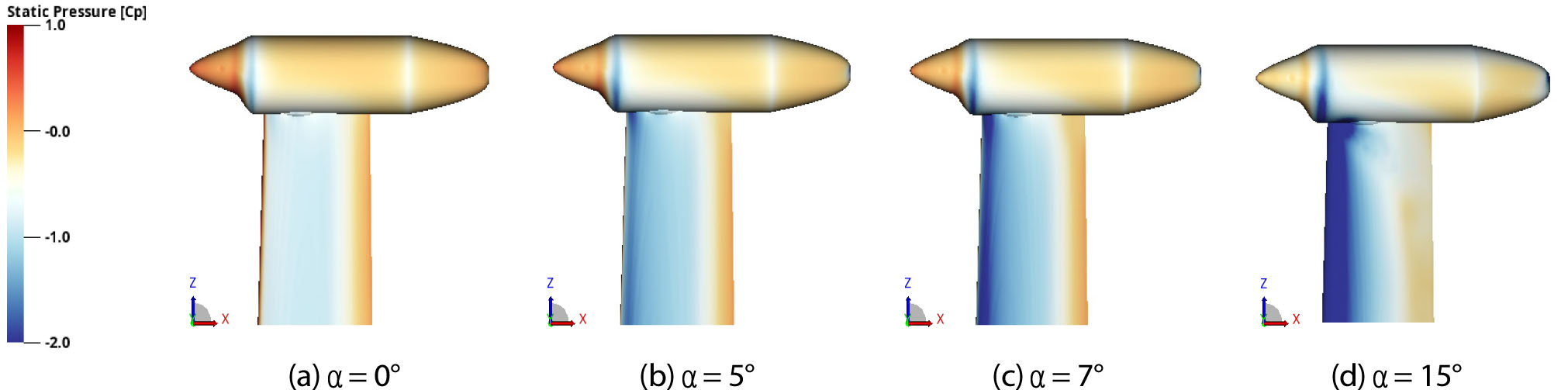
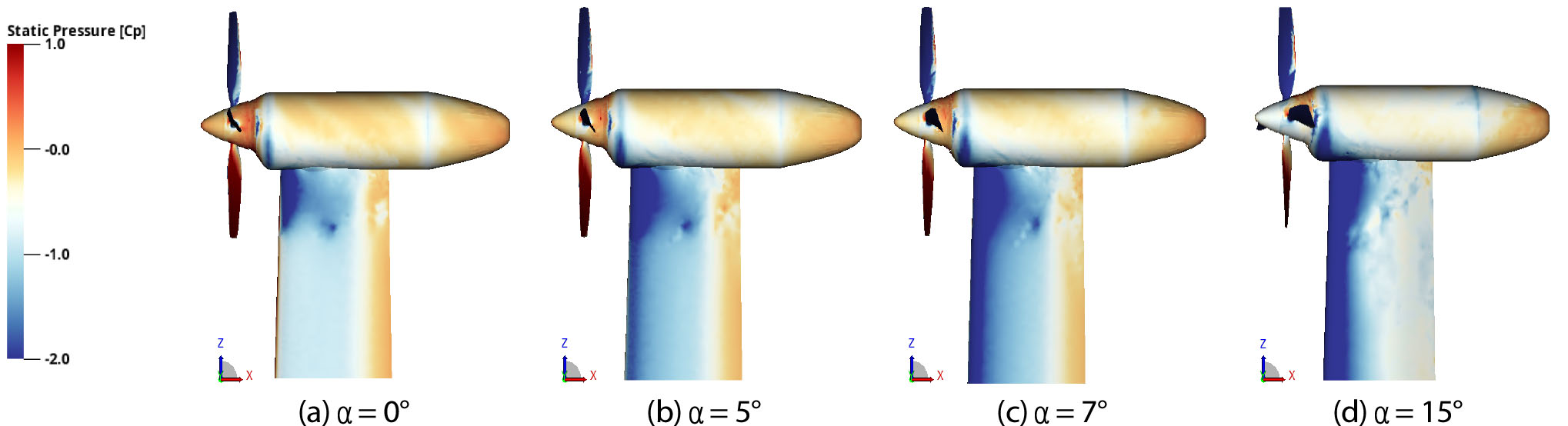
프로펠러에서 발생한 후류로 인한 날개 표면 압력 변화는 Fig. 8과 Fig. 9를 통해서도 확인할 수 있다. Fig. 8과 Fig. 9에서는 앞서 Fig. 6과 Fig. 7에서 고찰한 것과 같이 날개 표면 압력 해석 결과의 윗면 표면 압력 분포를 프로펠러 장착 여부에 따라 Static Pressure Contour 형태로 나타내었다. 프로펠러가 장착되지 않은 Isolated Wing 경우, 날개의 받음각이 커질수록 날개의 앞전에서 Suction Peak의 세기가 증가하였고, 날개 스팬 길이 방향으로 일정한 압력 분포가 발달하는 것을 확인하였다. 반면, 프로펠러가 장착된 Full Configuration의 경우, 날개 스팬 길이 방향 압력 분포가 일정하지 않게 나타나는 특성이 나타났다. 이는 프로펠러에서 발생한 후류로 인하여 날개 표면 압력계수가 일정하지 않은 것을 의미하며 Fig. 7(a)과 동일한 결과를 보여준다. 또한 프로펠러 회전으로 발생하는 후류로 인해 프로펠러 회전 수직 방향으로 압력이 더 낮게 나타나는 경향성을 관찰할 수 있다. 이는 프로펠러 후류가 날개 앞전 영역 유동의 속도를 가속 시켜 발생하는 것으로 판단된다.
Table 3 에는 받음각의 변화 및 프로펠러의 장착 여부에 따른 양력계수, 항력계수, 양항비를 해석하여 나타내었다. 날개 받음각 0°, 5°, 7°, 15°에서의 양력계수와 항력계수를 계산하였으며 날개의 받음각이 커짐에 따라 점진적으로 증가하는 것을 확인하였다. 프로펠러가 장착된 Full Configuration의 경우, 날개의 양력은 프로펠러가 장착되지 않은 Isolated Wing보다 평균적으로 4~5% 높게 나타났으며 항력은 최대 20%까지 높게 나타났다. 이러한 결과는 Fig. 6, Fig. 7에서 언급한 날개의 표면 압력 차이에 의한 것으로 판단되며, 특히 항력의 경우에는 받음각이 증가함에 따라 유도항력 증가로 인하여 더 큰 영향을 받는 것으로 확인하였다. 이를 통해 프로펠러의 후류는 날개의 양력과 항력에도 영향을 미치는 것을 확인할 수 있다.
Table 3.
Comparison of lift, drag, L/D coefficients between isolated wing and full configuration
3.2 상호작용이 날개 주변 유동장에 미치는 영향
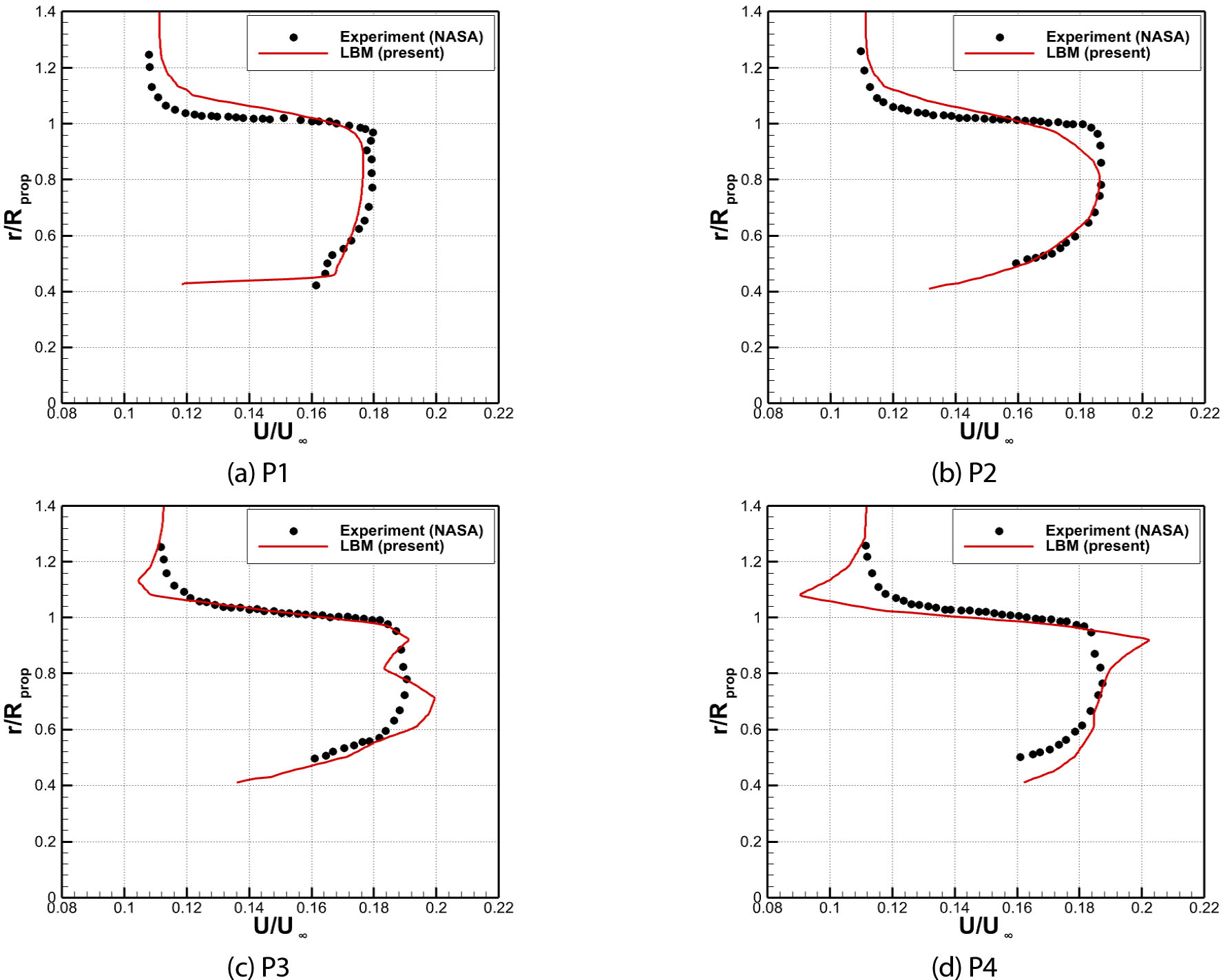
상호작용으로 인한 날개 주변 유동장을 확인하기에 앞서 프로펠러에서 발생하는 후류의 영향으로 발달하는 날개 주변의 속도장을 검증하였다. Fig. 10은 후류에 의해 변화되는 속도장을 Nacelle 길이 방향으로 속도분포를 계산하고 실험 데이터와 비교하였다[29]. 해당 위치는 Fig. 5를 통해 확인할 수 있으며, 자세한 위치는 Table 2와 같다. 비록 국소적으로 실험값과 비교하여 약 5~8% 오차가 발생하였지만, 전반적으로 모든 위치에서 실험값과 유사한 결과를 도출할 수 있었다. 특히 Nacelle의 거리와는 상관없이 최대 속도의 크기가 실험값과 유사하였고, 이를 통해 LBM 해석이 프로펠러의 후류를 잘 모델링할 수 있음을 확인하였다. 다만, Fig. 10(c), 10(d)에서 확인할 수 있듯이 프로펠러로부터 멀리 떨어진 P3, P4 위치에서는 프로펠러 후류가 하류 방향으로 전파됨에 따라 소산되는 정도에 대한 예측에 오차가 발생하였고, 이에 따라 속도 분포가 실험값과 다소 차이가 존재하였다.
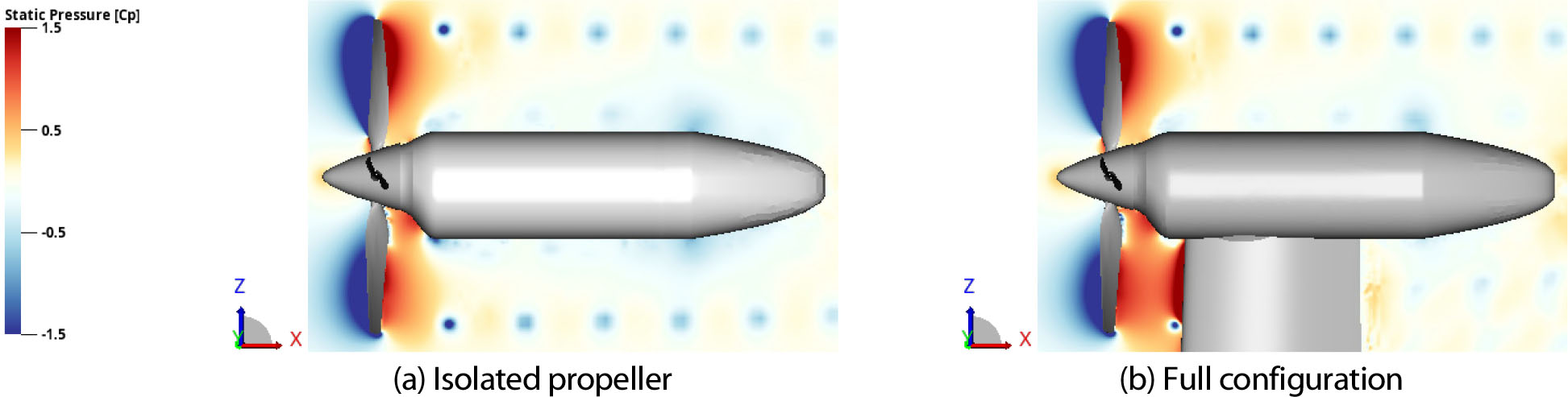
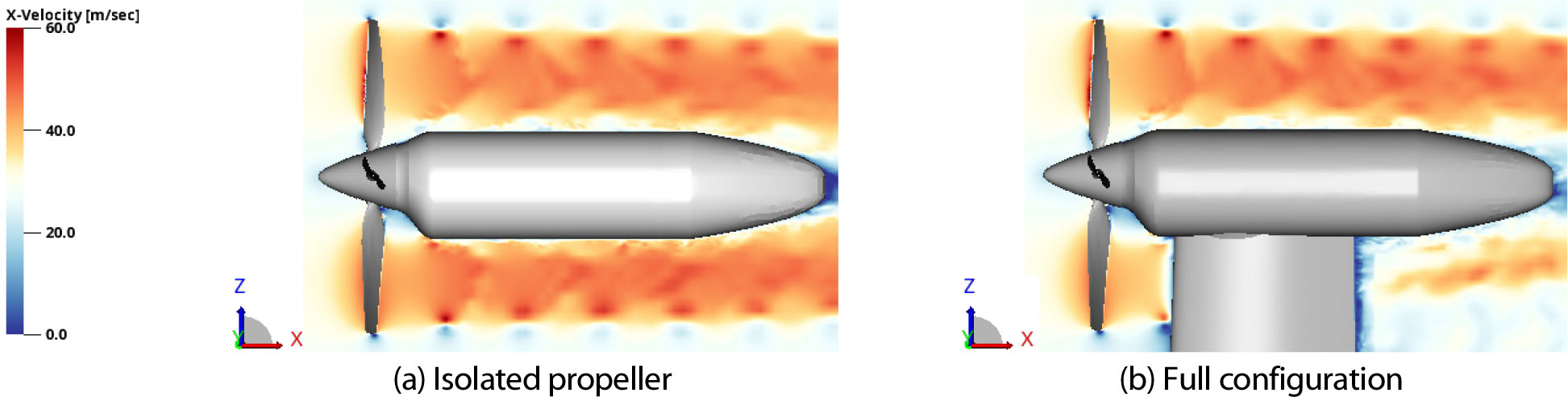
프로펠러 후류가 날개 장착 여부에 따라 날개 주변의 유동장에 미치는 영향을 고찰하기 위해, 프로펠러가 날개 위를 지나는 시점을 기준으로 Fig. 11과 Fig. 12에서 압력장과 속도장을 비교하였다. 날개가 없는 Isolated Propeller의 경우, 프로펠러 회전 방향으로 대칭적인 압력 분포가 발달하는 것을 확인할 수 있다. 또한 회전축 방향 속도(X-Velocity) 분포를 통해 프로펠러 후류에 의해 발달하는 유도 속도 성분을 확인할 수 있다. 반면 날개가 존재하는 Full Configuration의 경우, 프로펠러가 날개 위를 지날 때 프로펠러와 날개 사이의 압력이 증가하는 영역이 넓어지는 현상이 나타났다. 또한 프로펠러가 장착된 날개 끝단에서의 유동 속도가 감소하는 경향성을 관찰할 수 있다. 이러한 현상은 프로펠러 후류가 날개와 충돌하며 속도가 감소하기 때문에 발생했으며, 날개와 근접한 표면에서 X축 방향 속도가 0에 가까워짐을 Fig. 12(b)에서 확인할 수 있다.
3.3 상호작용이 프로펠러 공력 특성에 미치는 영향
앞선 결과들에서는 상호작용 효과가 날개의 공력 및 유동장 특성에 미치는 영향을 분석하였다. 프로펠러-날개 상호작용 효과가 프로펠러의 공력 특성에 미치는 영향을 고찰하기에 앞서 받음각 0° 조건에서 프로펠러의 추력과 토크 비교를 통해 LBM 해석자를 검증하였다. 실험 결과와의 비교를 위해 식 (9), (10)을 이용하여 프로펠러의 추력 및 토크 계수를 계산하였다. Table 4에서 확인할 수 있듯이 LBM 해석 결과가 시험 결과와 비교하여 추력 계수는 1.51% 과대 예측, 토크 계수는 약 4.3% 과소 예측하였다. 토크 계수 예측에 다소 오차가 존재하였지만, 프로펠러의 공력 성능을 오차율 5% 이내로 실험 데이터와 유사한 결과를 도출할 수 있었다. 해당 결과는 동일 모델을 다른 해석자로 예측한 선행 연구 결과에도 오차율 2~5% 이내로 LBM 해석자와 비슷한 경향성을 가진다[28].
Table 4.
Comparison of thrust and torque coefficients with experimental data
| Coefficient | Experiment | LBM simulation | Error |
| CT | 0.391 | 0.397 | 1.51% |
| CQ | 0.0485 | 0.0465 | 4.30% |
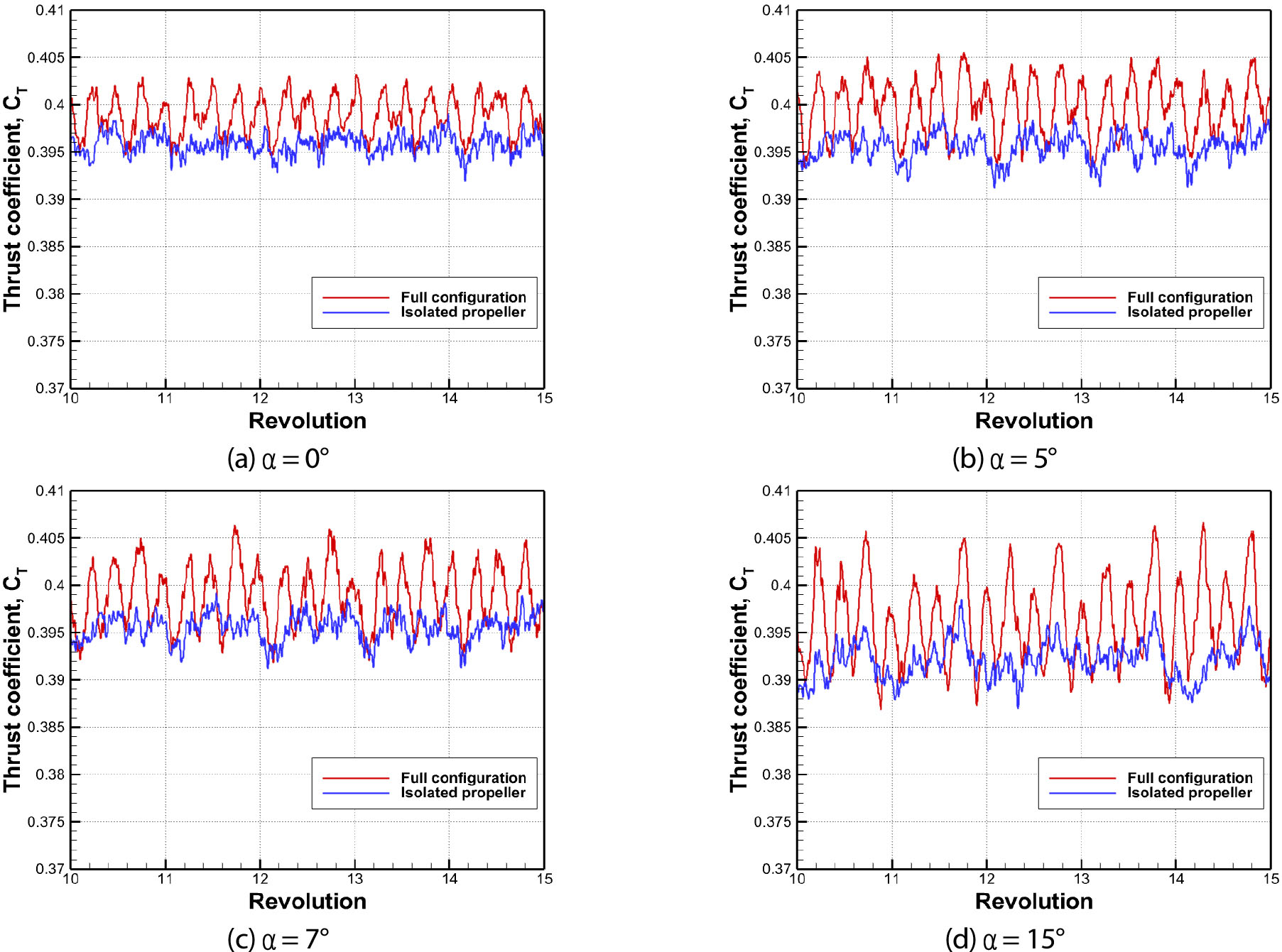
날개의 장착 여부가 프로펠러의 추력 계수에 미치는 영향을 분석하여 Fig. 13에 나타내었다. 총 회전수 15바퀴 중 마지막 5바퀴에 대한 프로펠러의 추력 계수 값을 비교하였다. 날개를 장착한 Full Configuration 프로펠러의 경우, 장착하지 않은 Isolated Propeller보다 모든 받음각에서 2~3% 높은 추력 계수가 해석되었다. 이러한 추력 계수 증가는 Fig. 11에서 확인할 수 있듯이 날개가 프로펠러의 후류를 차단하며 프로펠러 후면의 압력이 높아졌기 때문이다. Fig. 11과 Fig. 12에서 관찰한 바와 같이 Isolated Propeller의 추력 계수는 주기적으로 파동이 발생하는 반면 Full Configuration에서 프로펠러의 추력 계수는 Isolated Propeller인 경우보다 진폭이 크게 해석되었다. 이는 프로펠러의 블레이드가 날개 앞전을 지나는 순간 상호작용하며 발생하는 것으로 판단된다.
3.4 상호작용이 프로펠러 후류 구조에 미치는 영향
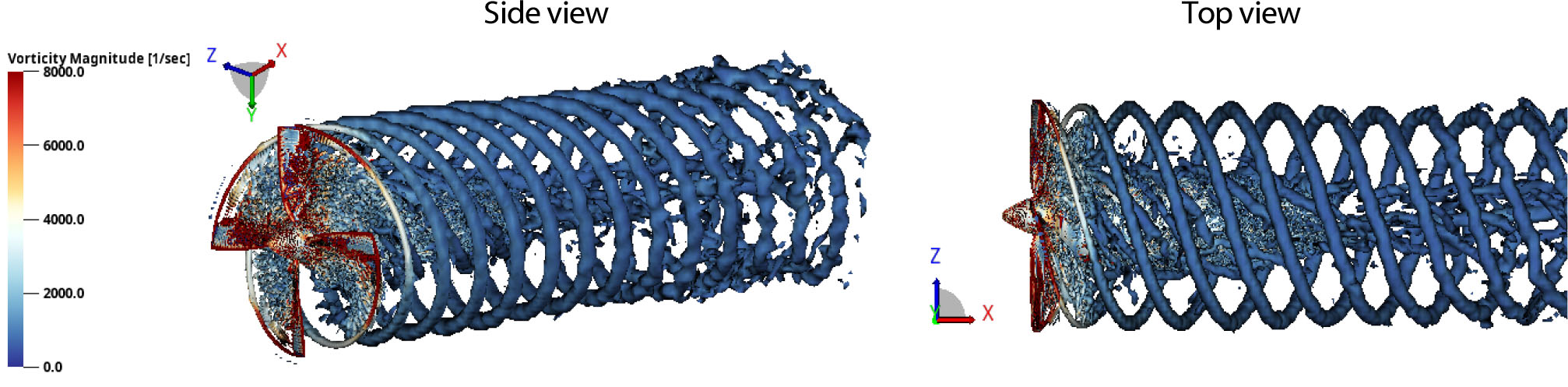
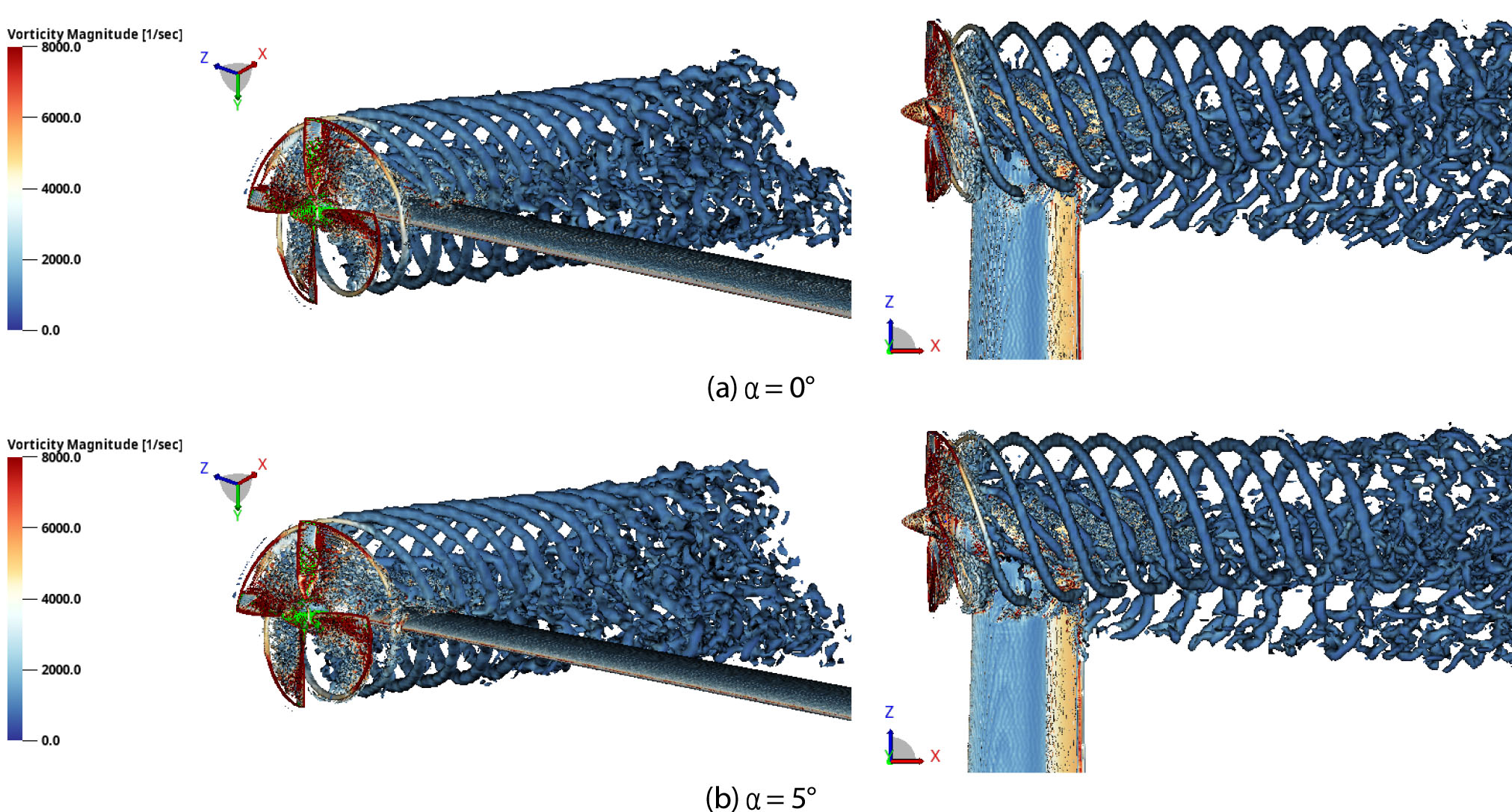
날개 장착 여부가 프로펠러의 후류 구조에 미치는 영향을 분석하기 위하여, 날개의 받음각 0°, 5°, 7°, 15°에 따른 프로펠러의 후류 구조를 Fig. 14과 Fig. 15에 날개 기준 Side View와 Top View로 나타내어 비교하였다. 날개가 없는 Isolated Propeller의 후류 구조는 Fig. 14에 나타나며, Fig. 15는 날개가 존재하는 Full Configuration의 후류 구조를 날개의 받음각에 따라 나타내었다. Isolated Propeller의 경우 나선형 형태의 뚜렷한 후류 구조가 회전 방향으로 발달하는 모습을 확인할 수 있다. 또한 후류 진행 방향으로 방해하는 요인이 없으므로 대칭적인 구조가 나타난다. 하지만 Full Configuration의 경우 후류의 구조가 비대칭적으로 발달하며, 날개의 받음각이 커짐에 따라 후류 구조가 소산 되는 현상이 조기에 발생함을 관찰하였다. 또한, 날개의 받음각이 커짐에 따라 날개 윗면의 뒷전에서 발달한 박리 유동과 프로펠러 후류가 강한 상호 간섭 현상이 발생하였고, 특히 받음각 15° 조건에서는 하류 방향에 상당히 복잡한 형태의 구조가 발달하는 것을 확인할 수 있었다.
4. 결 론
본 연구에서는 LBM 기반의 소프트웨어인 PowerFLOW를 사용하여 날개 유무와 프로펠러 유무에 따른 공력 특성에 관한 검증과 해석을 수행하였다. 해석자 검증을 위해 NASA의 WIPP 실험 데이터를 활용하였다. Full Configuration의 프로펠러 추력 계수와 토크 계수를 비교하였으며, 날개 스팬 위치에 따른 표면 압력, 속도를 비교 검증하였다. 이를 통하여 LBM 해석이 실험 데이터와 상당히 유사한 결과를 도출할 수 있음을 확인하였다.
날개와 프로펠러의 상호작용 현상이 날개의 양력 성능, 후류 구조 발달, 표면 압력에 미치는 영향을 전산해석을 통해 분석하였다. 프로펠러 후류의 효과로 인해 날개 윗면에서의 Suction Peak의 세기가 증가하였고, 이로 인해 양력 향상(Lift Augmentation)이 발생하는 것을 확인하였다. 또한 날개의 존재가 프로펠러 후류 발달에 영향을 미치는 것을 확인하였으며, 프로펠러가 날개 위를 지나는 경우 회전축의 수직 방향으로 날개 주변에 강한 압력장이 형성되어 프로펠러의 추력 값이 증가함을 확인하였다.
본 연구를 통해 LBM 해석은 프로펠러와 날개 간의 공력해석 연구에 활용될 수 있음을 확인하였으며 프로펠러와 날개의 공기역학적 상호작용에 대한 분석을 진행하였다. 현재 연구에서는 Wingtip Mounted Propeller에 따른 날개와 프로펠러에 미치는 영향을 중심으로 연구하였으나 향후 연구에서는 다수의 프로펠러가 적용된 형상에 대한 해석을 수행하여 DEP 시스템상에서 발생하는 공력 특성에 대해 고찰하고자 한다. 추가적으로 날개-프로펠러 간의 상호작용이 소음에 미치는 영향을 고려할 예정이다.