BOUNDARY LAYER TRANSITION MODEL WITH COMPRESSIBILITY CORRECTION FOR TRANSONIC FLOW SIMULATIONS

J.B. Hong; Y.S. Jung

doi:10.6112/kscfe.2024.29.2.013

Preview

Original Article

Journal of Computational Fluids Engineering. 30 June 2024. 13-33
https://doi.org/10.6112/kscfe.2024.29.2.013

BOUNDARY LAYER TRANSITION MODEL WITH COMPRESSIBILITY CORRECTION FOR TRANSONIC FLOW SIMULATIONS

압축성 효과 보정을 적용한 경계층 천이 모델의 천음속 유동해석

J.B. Hong¹

Y.S. Jung¹^†

홍 지범¹

정 용수¹^†

¹Department of Aerospace Engineering, Pusan National University

¹부산대학교 항공우주공학과

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted noncommercial use, distribution, and reproduction in anymedium, provided the original work is properly cited.

ABSTRACT

The Medida-Baeder laminar-turbulent boundary layer transition model, based on Reynolds-averaged Navier-Stokes, has been extended by applying an existing compressibility correction. The correction was derived from the stability analysis of Tollmien-Schlichting instabilities and developed for the Langty-Menter transition model. Performance of the extended model was evaluated through the transonic flows over VA-2 and CAST10-2 airfoils where the compressible effects prevail. With the extended model, the prediction of transition onset is delayed, resulting in improved agreement with experimental data from the baseline model in skin friction distribution. Furthermore, the extended model was applied to the challenging NASA Common Research Model-Natural Laminar Flow wing-body configuration under transonic flight conditions. Sectional pressure coefficients and transition locations were compared with experimental results at various angles of attack. The prediction accuracy in transition onset along the wing span is improved, which are comparable with the predicting result from linear stability theory based transition model.

Keywords

Boundary layer transition model

Compressibility correction

Transonic flow

Common Research Model-Natural Laminar Flow

키워드

경계층 천이 모델

압축성 효과 보정

천음속 유동

CRM-NLF

MAIN

1. 서 론
2. 수치 방법
2.1 압축성 효과 보정식
2.2 압축성 효과 보정식을 적용한 Medida-Baeder 천이 모델
2.3 해석 솔버
3. 검증 및 해석
3.1 아음속 익형 해석 및 검증
3.2 천음속 익형 해석 및 검증
4. 결 론

1. 서 론

경계층 천이(boundary layer transition)는 층류에서 난류로의 상태 변화를 의미하며, 난류 경계층은 물체의 표면 마찰력을 증가시키므로 전체 항력증가의 원인이 된다[1]. 항공산업에서 연료의 효율성을 높이기 위해 Natural Laminar Flow(NLF) 익형을 날개에 적용하고, 경계층 천이를 지연시킴으로써 항력을 최소화하는 연구가 있다. 특히 Wilson 외 등[2]과 Allison 외 등[3]에서는 NLF 익형 설계 기술을 적용한 차세대 항공기는 10~15%의 연료 효율을 증가시킬 것으로 기대하였다. 항공기 최적 설계 단계에서 경계층 천이 현상을 고려한 효율적이고 정확한 공력 예측을 위해 주로 Reynolds-Averaged Navier-Stokes(RANS) 기반의 경험적 상관관계식인 $γ - {\tilde{R e}}_{θ t}$ (Langtry-Menter 2009, LM2009) 천이 모델이[4] 사용된다. 대표적으로 Han 외 등[5]의 NLF 날개 형상 최적화에 적용되었고 Thurman 외 등[6] 로터 블레이드 최적화 형상 설계를 위한 인공신경망 학습에 사용된 사례가 있다.

$γ - {\tilde{R e}}_{θ t}$ 모델은 아음속 영역 기반의 경험적 모델로 아음속 영역의 익형 및 비행체 형상에 대해 정확한 천이 지점을 예측할 수 있다. 초기 모델의 경우 이차원 경계층의 Tollmien-Schlichting(T-S) 불안정성에 의한 천이 예측만 가능하였지만[4], 다양한 선행연구를 통해 삼차원 경계층 유동에 의한(crossflow-induced) 불안정성[7]과 표면 거칠기에 의한(roughness-induced) 천이 예측[8]으로 모델의 적용 가능한 해석 영역이 확장되었다. Arnal 외 등[9]은 선형 안정성 이론(Linear Stability Theory)에 의해 천음속 영역에서 마하수가 증가함에 따라 경계층 안정성의 증가와 T-S 불안정성 증폭률의 감소로 경계층 천이가 지연되는 효과를 보여주었지만 $γ - {\tilde{R e}}_{θ t}$ 모델은 천음속 영역에서 지배적인 압축성 효과를 기대하기 힘들다[10]. 따라서, 천음속 비행 조건에서 경계층 천이 현상에 따른 항공기의 성능을 예측함에 있어서 RANS 기반의 해석 방법에는 한계가 있다.

2021 AIAA Transition Modeling and Prediction Workshop[11]에서 NASA Common Research Model – Natural Laminar Flow(CRM–NLF) 날개 및 동체 형상에 대한 다양한 RANS 기반의 천이 모델 평가가 이루어졌다. 천음속( $M a$ =0.86) 유동 조건에서 받음각에 따른 날개 윗면의 천이 지점 및 익형 압력 분포 등을 풍동실험 결과와 비교 하였다. 선형 안정성 이론 기반의 $e^{N}$ 모델을 제외한, 경험적 상관관계식 기반의 천이 모델들은 모두 천이 지점을 일찍 예측하는 결과를 보여주었다.

이후 경험적 상관관계식 기반의 천이 모델 중 하나인 $γ - {\tilde{R e}}_{θ t}$ 모델에 압축성 효과 보정식을 적용하는 연구가 수행되었고, 천음속 영역에서 천이 지점 예측의 개선을 보였다. 대표적으로 Piotrowski 외 등[12]은 지역 변수를 사용하는 Arnal-Habiballah-Delcourt(AHD) simple 모델[13]을 이용하여 T-S 불안정성에 의한 천이 메커니즘에 해당하는 압축성 효과 보정식을 $γ - {\tilde{R e}}_{θ t}$ (Langtry-Menter 2015, LM2015) 천이 모델[7]에 적용하였다. 또한, 천음속 익형의 해석을 통해 압축성 효과 보정식의 상수를 조절하여 수정된 압축성 효과 보정식을 제시하였다. Venkatarchari 등[14]은 NASA CRM-NLF 형상의 해석에서 $e^{N}$ 모델을 이용해 날개 윗면의 천이 위치에 대한 T-S와 crossflow 천이 메커니즘에 의한 효과의 크기인 N-factor를 제시하였고 crossflow의 천이 효과가 크지 않음을 제시하였다. 그리고 Qiao 외 등[15]의 압축성 효과 보정식을 LM2015 모델[7]에 적용하였고 Amplification Factor Transport(AFT) 모델에 Sturdza[16]의 압축성 효과 보정식을 적용하여 두 가지 천이 모델을 이용한 NASA CRM–NLF 형상 해석을 진행하였다.

이처럼 RANS 기반의 경험적 상관관계 천이 모델을 이용한 천음속 영역 NASA CRM-NLF의 해석에 대한 한계점과 이를 극복하고자 압축성 효과를 적용하는 연구가 최근 활발하게 이루어졌고 경계층 천이 위치의 정확도 향상의 도전적 과제가 되었다. 따라서 본 연구에서는 선행연구를 통해 검증된 Medida-Baeder 천이 모델에 압축성 효과 보정식을 적용하고자 한다. 우선, 압축성 효과 보정식을 천음속 영역 익형 해석을 통해 검증하여 결합이 타당함을 보이고 NASA CRM-NLF 형상에 적용하여 개선된 천이 지점 예측을 보여주고자 한다.

2. 수치 방법

2.1 압축성 효과 보정식

본 연구에는 $γ - {\tilde{R e}}_{θ t}$ (LM2015) 모델[7]에 적용되어 검증된 Piotrowski 외 등[12]에 의해 개발된 압축성 효과 보정식을 적용하였다. 보정식은 Perraud 외 등[13]의 지역 변수를 사용하는 AHD simple 모델을 기반으로 개발되었고, AHD simple 모델은 Arnal 외 등[17]의 압축성 효과가 고려되고 경계층 안정성 이론 기반의 광역 변수를 사용하는 AHD 모델로부터 파생되었다.

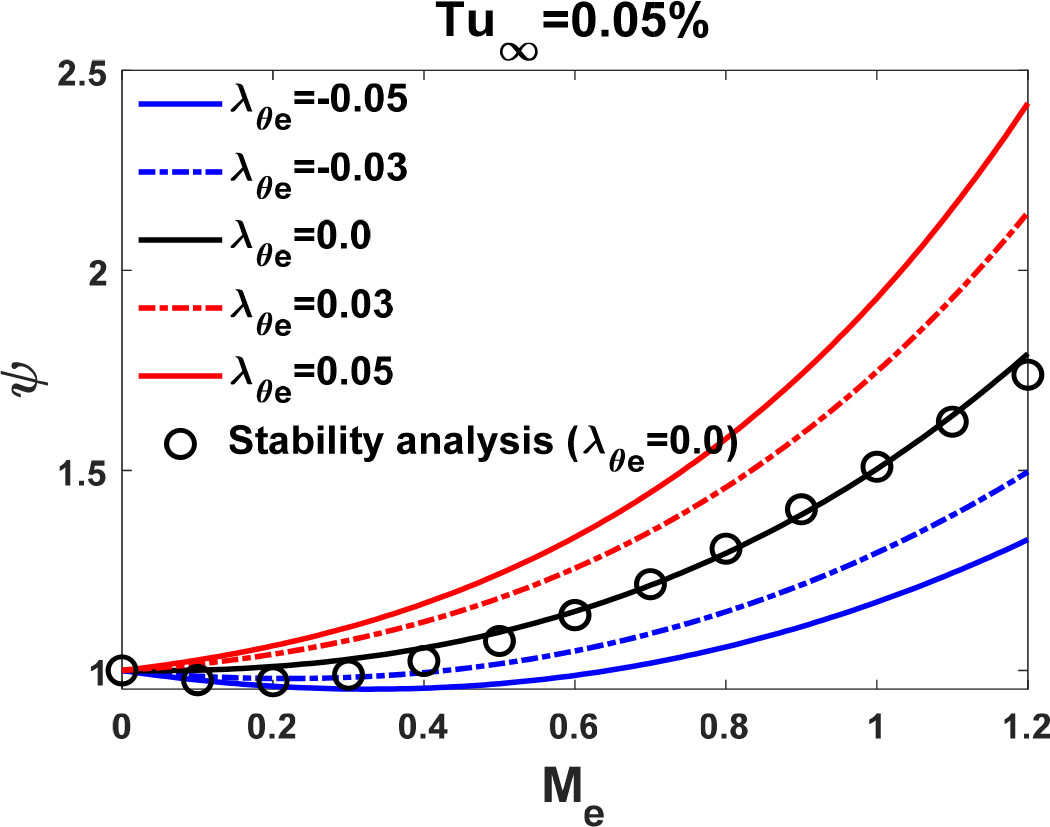
Fig. 1은 자유류 난류강도 0.05%, 영 압력구배 조건의 유동에 대해서, AHD simple 모델[13]과 $γ - {\tilde{R e}}_{θ t}$ (LM2009) 모델[6]의 경계층 마하수( $M_{e}$ )에 대한 경계층 천이 지점의 운동량 두께(momentum thickness) 레이놀즈 수( $R e_{θ t}$ )를 경계층 안정성 모델[17]에 대해 비교한 그래프이다. 본 결과 사용된 각각의 모델에 대한 자세한 식들은 참고문헌에 나타나있다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F1.jpg

Fig. 1.

Transition onset momentum thickness Reynolds number as a function of boundary layer Mach number at zero pressure gradient

AHD simple 모델[13]은 Arnal 외 등[17]의 경계층 안정성 계산 결과와 잘 일치한다. 반면, LM2009 모델[4]은 경계층 마하수 $M_{e}$ 에 대해 고려되지 않아 $R e_{θ t}$ 가 일정한 값을 갖는 것을 알 수 있다. 따라서 LM2009 모델[4]은 경계층 마하수 증가에 따른 경계층 안정화가 고려되지 않기 때문에 천음속 영역에서 상류 위치에 빠른 천이를 예측한다. 본 연구에 사용된 압축성 효과 보정식은 식 (1)과 같고 Piotrowski 외 등[12]의 초기 모델에 해당한다.

(1)

ψ = (a_{1} M_{c}^{2} + a_{2} M_{c} + a_{3}) \exp [b_{1} λ_{θ c} M_{c}] \exp [(c_{1} + c_{2} \sqrt{T u_{\infty}}) M_{c}] where a_{1} = 0.44, a_{2} = - 0.38, a_{3} = 1.0, b_{1} = 5.0, c_{1} = 0.41, c_{2} = - 0.27

식 (1)과 같이 압축성 효과 보정식은 경계층 마하수( $M_{e}$ ), 압력구배 파라미터( $λ_{θ e}$ ), 자유류 난류강도( $T u_{\infty}$ )로 이루어졌다. 여기서 경계층 마하수( $M_{e}$ )는 식 (2)과 같이 정의 되며, $a_{e}$ 와 $U_{e}$ 는 각각 경계층 음속과 유동 속도를 나타낸다. 식 (3)과 (4)는 베르누이 방정식의 등엔트로피 관계식을 통해 계산된다. 여기서 𝛾는 유동장의 비열비를 나타낸다. 또한, AHD simple 모델 조건에 의해 경계층 마하수 1.1 이하, 자유류 난류강도 크기 1% 미만의 외부유동에 적용 가능하다[12,13].

(2)

M_{e} = U_{e} / a_{e}

(3)

a_{c} = \sqrt{\frac{γ P_{\infty}}{ρ_{\infty}} {(\frac{P}{P_{\infty}})}^{1 - 1 / γ}}

(4)

U_{c} = \sqrt{U_{\infty}^{2} + \frac{2 γ}{γ - 1} \frac{P_{\infty}}{ρ_{\infty}} [1 - {(\frac{P}{P_{\infty}})}^{1 - 1 / γ}]}

(5)

λ_{θ c} = \frac{ρ θ^{2}}{μ} \frac{d U_{c}}{d s}

(6)

\begin{aligned} \frac{d U_{c}}{d s} = [(\frac{u}{U}) \frac{d U_{c}}{d x} + (\frac{v}{U}) \frac{d U_{c}}{d y} + (\frac{w}{U}) \frac{d U_{c}}{d z}] \\ where \{\begin{cases} \frac{d U_{c}}{d x} = - \frac{1}{ρ_{\infty} U_{c}} {(\frac{P}{P_{\infty}})}^{- 1 / γ} \frac{d P}{d x} \\ \frac{d U_{c}}{d y} = - \frac{1}{ρ_{\infty} U_{c}} {(\frac{P}{P_{\infty}})}^{- 1 / γ} \frac{d P}{d y} \\ \frac{d U_{c}}{d z} = - \frac{1}{ρ_{\infty} U_{c}} {(\frac{P}{P_{\infty}})}^{- 1 / γ} \frac{d P}{d z} \end{cases} \end{aligned}

식 (5)의 압력구배 파라미터( $λ_{θ e}$ )는 식 (6)에 해당하는 유동 방향의 압력구배로 이루어져 순 압력구배에는 양의 크기로 증가하고 역 압력구배에는 음의 크기로 증가하는 특징을 갖는다. 또한 $λ_{θ e}$ 는 수치적 강건성을 위해 LM2009의 $λ_{θ}$ 와 같은 –0.1≤ $λ_{θ e}$ ≤0.1의 범위를 갖는다[12]. 여기서 경계층 운동량 두께(𝜃)는 운동량 두께 레이놀즈 수( ${\tilde{R e}}_{θ t}$ ) 수송 방정식에서 Newton Raphson 방법과 같은 반복법으로 구해진다[4].

Fig. 2는 $λ_{θ e}$ 의 변화에 따라 경계층 마하수( $M_{e}$ )에 대한 압축성 효과 보정값의 경향성을 보인다. 우선, 영 압력구배 조건에서 본 압축성 효과 보정식은 경계층 안정성 모델[17]에 부합하다. $λ_{θ e}$ 가 0.03, 0.05와 같이 순 압력구배에서 $M_{e}$ 가 증가할수록 압축성 효과 보정값(𝜓)이 커지게 되고. -0.03, -0.05와 같이 역 압력구배 상황에서 보정값(𝜓)이 작아지면서 같은 $M_{e}$ 조건인 천음속 영역에서 압축성 효과에 의한 안정화가 상대적으로 작다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F2.jpg

Fig. 2.

The compressibility correction as a function of boundary layer Mach number and pressure gradient

2.2 압축성 효과 보정식을 적용한 Medida-Baeder 천이 모델

본 연구에 사용된 Medida-Baeder(M-B) 천이 모델[18]은 $γ - {\tilde{R e}}_{θ t}$ 기반의 경험적 모델로 Spalart-Allmarse(S-A) 난류 모델에 결합되어 사용된다. 다양한 선행 연구를 통해 검증되었으며, 삼차원 경계층(crossflow-induced) 및 표면 거칠기에 의한 천이 효과를 고려할 수 있다[19]. 본 연구에서는 아래 식 (7, 8, 9, 10, 11, 12, 13) 과 같이 난류 간헐도(𝛾) 수송 방정식에 압축성 효과 보정식(𝜓)을 식 (11)과 같이 적용하였다.

(7)

\frac{D (ρ γ)}{D t} = P_{γ} - D_{γ} + \frac{\partial}{\partial x_{j}} [(μ + μ_{t}) \frac{\partial γ}{\partial x_{j}}]

(8)

P_{γ} = \{\begin{cases} γ \leq 1.0, ρ F_{onset} G_{onset} max [\frac{Ω}{F_{length}}, \frac{1.0}{F_{length, min}}] \\ γ > 1.0, 1.0 - γ \end{cases}

(9)

D_{γ} = ρ Ω γ (1.0 - G_{o n s e t})

(10)

F_{o n s e t} = \max (F_{o n s e t 2} - F_{o n s e t 3}, 0)

(11)

F_{o n s e t 1} = \frac{R e_{v}}{2.193 (ψ R e_{θ c})}

(12)

F_{o n s e t 2} = \min (\max (F_{o n s e t 1}, F_{o n s e t 1}^{2}), 4.0)

(13)

F_{o n s e t 3} = \max (2.0 - (0.25 R_{T})^{3}, 0)

식 (8), (9)는 난류 간헐도(𝛾) 수송 방정식의 생성항과 소멸항으로 𝛺는 와도의 크기를 나타내고 $F_{l e n g t h}$ 는 천이 구간의 길이를 조절해 주는 상수로 10.0의 값을 가지고 $F_{l e n g t h, m i n}$ 은 2.5의 값을 가진다[19]. 식 (8), (9)의 $G_{o n s e t}$ 은 전역변수로써 난류 간헐도(𝛾) 수송 방정식의 생성항과 소멸항의 스위치 작용을 하게 되며, 식 (10)의 $F_{o n s e t}$ 은 $G_{o n s e t}$ 과 같이 난류 간헐도 (𝛾) 수송 방정식의 생성항의 스위치 작용을 해주는 변수이다. 자세한 내용은 선행연구 [18,19]을 참조할 수 있다.

식 (11)과 같이 압축성 효과 보정식(𝜓)은 $R e_{θ c}$ 항에 곱해짐으로써 임계 운동량 두께 레이놀즈 수를 증가시키는 효과를 주게 되며, 이는 경계층 내 안정성 효과가 증대시켜 천이의 지연을 유도한다. 본 압축성 효과 보정방법은 Piotrowski 외 등[12]을 따르며, 운동량 두께 레이놀즈 수( ${\tilde{R e}}_{θ t}$ ) 수송방정식의 경우 Jung 외 등[19]의 식과 같다.

2.3 해석 솔버

유동 해석 솔버의 경우 미국 메릴랜드 대학교(University of Maryland)에서 개발한 Reynolds-Averaged Navier-Stokes (RANS) 기반 Mercury Framework를 사용하였다[20]. 다중격자/다중솔버 로써, CRM-NLF의 삼차원 유동 해석을 위해 해당 모델 근처의 영역은 비정렬 격자 기반의 HAMSTR 솔버를 사용하고, 이외의 영역의 경우 정렬격자 기반의 GARFIELD 솔버를 사용하였다. 해석 영역/솔버 간 정보교환을 위해 중첩 격자기법을 적용하였다. 익형 유동해석의 경우 이차원 HAMSTR 솔버[21]만을 이용하여 해석을 진행하였다.

비점성 플럭스 계산을 위해 5차 정확도의 Weight Essentially Non-Oscillatory(WENO)를 사용하였고 점성 플럭스 계산은 2차 정확도의 중앙 차분법을 이용하여 공간 차분을 하였다. 시간 적분법으로 HAMSTR 솔버의 경우 Diagonally Dominant Line Gauss-Seidal(DDLGS)를 이용하였고 GARFIELD 솔버의 경우 Diagonalized Alternating Direction Implicit(DADI)를 사용하였다.

3. 검증 및 해석

3.1 아음속 익형 해석 및 검증

본 연구에 사용된 기존의 M-B 천이 모델에 대한 검증으로 낮은 받음각에서 자연 천이를 일으키는 NLF(1)-0416 익형과 낮은 레이놀즈 수에서 층류 박리거품과 박리 천이를 일으키는 Eppler 387 익형에 대한 해석 및 검증을 진행하였다.

3.1.1 NLF(1)-0416 익형

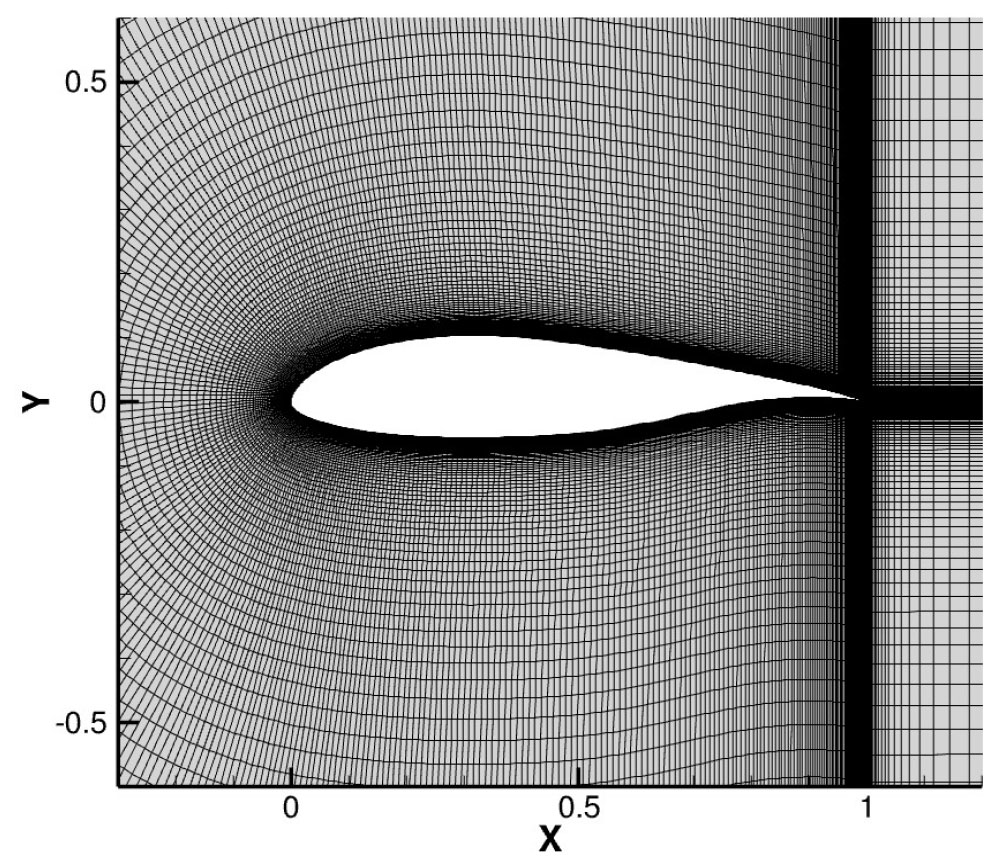
NLF(1)-0416 익형은 마하수 0.1 레이놀즈 수 $R e$ =4×10⁶으로 NASA Langley Research Center의 아음속 풍동실험[22]이 진행되었다. 자유류 난류강도는 0.15%이다[23]. NLF(1)-0416 익형의 격자는 Table 1과 같이 구성하였다. Fig. 3과 같이 C-type 정렬격자로 구성되었고 시위 길이의 100배에 해당되는 far-boundary 조건과 익형 표면은 no-slip 조건을 부여하였다. 익형 표면노드 수와 $y^{+}$ 에 의한 첫 번째 점성층은 Coarse, Medium, Fine 조밀성 단계에 따라 다르게 구성하였다. 받음각 -6°에서 6°의 연산을 진행하였다.

Table 1.

NLF(1)-0416 airfoil C-grid dimensions

Grid level	Surface nodes	$y^{+}$	First wall-normal grid spacing
Coarse	201	1.2	7.793×10^-6
Medium	401	0.8	5.195×10^-6
Fine	801	0.4	2.597×10^-6

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F3.jpg

Fig. 3.

NLF(1)-0416 airfoil configuration composed of the Medium resolution grid

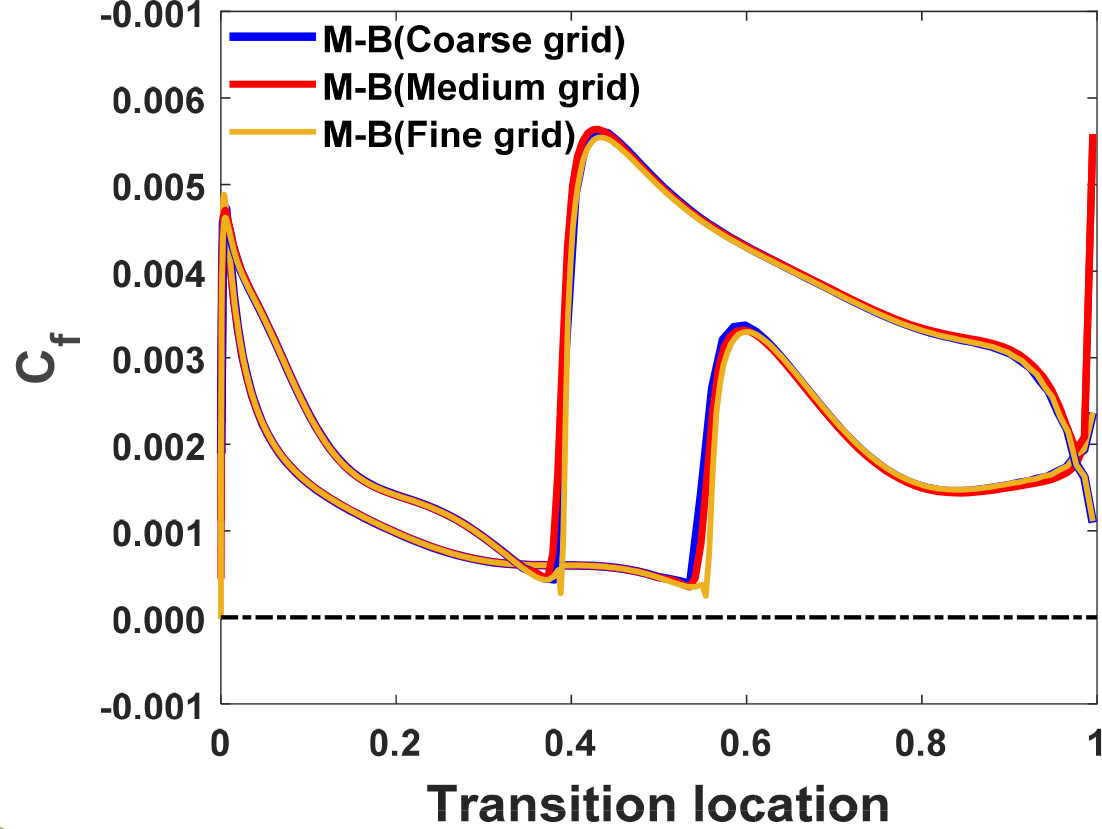
Fig. 4는 받음각 0°에서 격자 조밀성에 따른 익형 윗면과 아랫면의 표면 마찰계수를 비교하였다. Coarse, Medium, Fine 격자 모두 유사한 표면 마찰계수를 보여준다. 따라서 윗면과 아랫면 각각 $x / c$ =0.37, 0.54 위치에서 표면 마찰계수가 급격히 증가한다. 이때 유동은 순방향 속도를 갖게 되어 표면 마찰계수가 양수이므로 자연 천이를 예측하는 것을 알 수 있다. 또한, 받음각 -6°에서 6°까지 모든 범위에서 자연 천이가 나타나는 것을 확인하였고 모든 격자에 대해 동일한 표면 마찰계수를 보여주므로 Medium 격자에서 충분한 결과를 얻을 것으로 판단하였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F4.jpg

Fig. 4.

Skin friction coefficient of NLF(1)-0416 airfoil at an angle of attack of 0 degrees

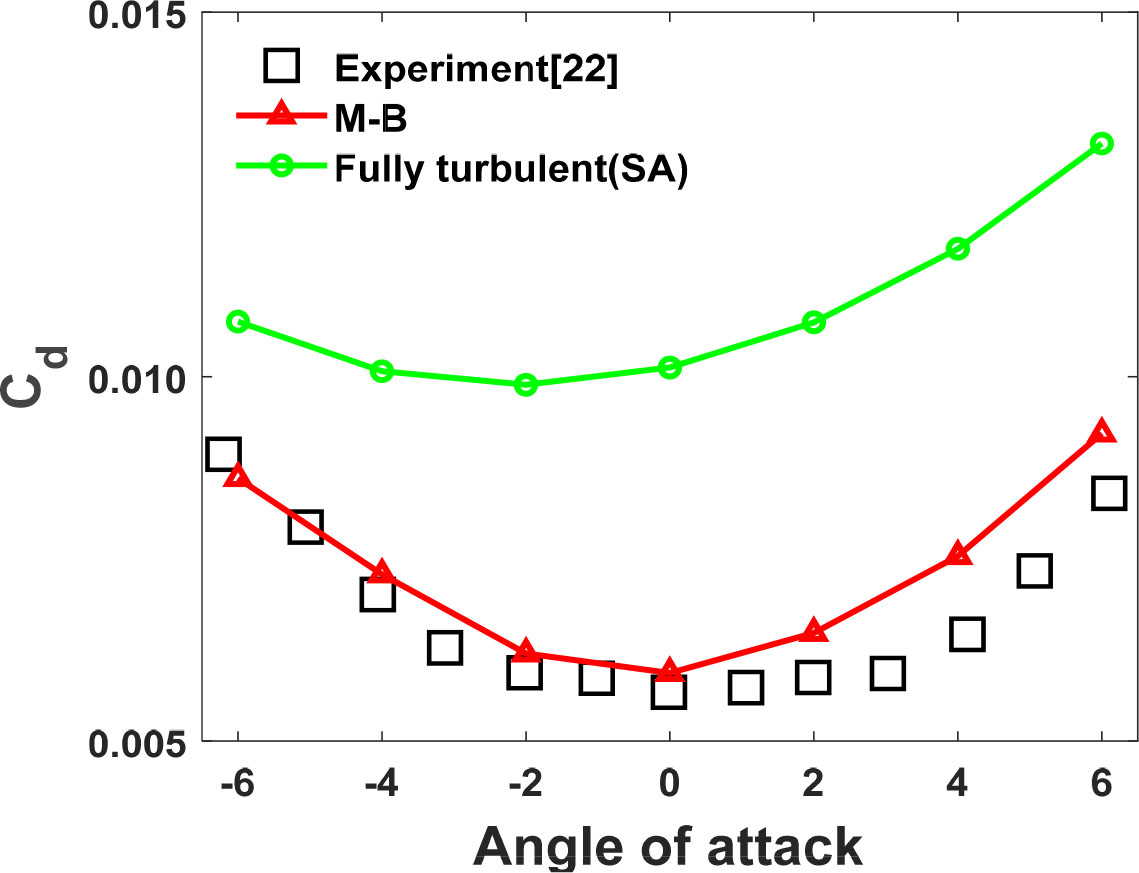
Fig. 5는 본 연구의 받음각에 따른 Medium 격자에 대한 항력계수의 결과를 실험값과 비교하였다. 저 받음각에서 실험값과 유사한 결과를 얻었으며 고 받음각에서 실험값과 동일한 경향성을 보여주는 것을 알 수 있다. 반면에 층류 경계층을 고려하지 않는 완전 난류 해석결과는 실험값에 크게 벗어났다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F5.jpg

Fig. 5.

Comparison of drag coefficients for the NLF(1)-0416 airfoil between the experiment and predictions(SA turbulence and transition models)

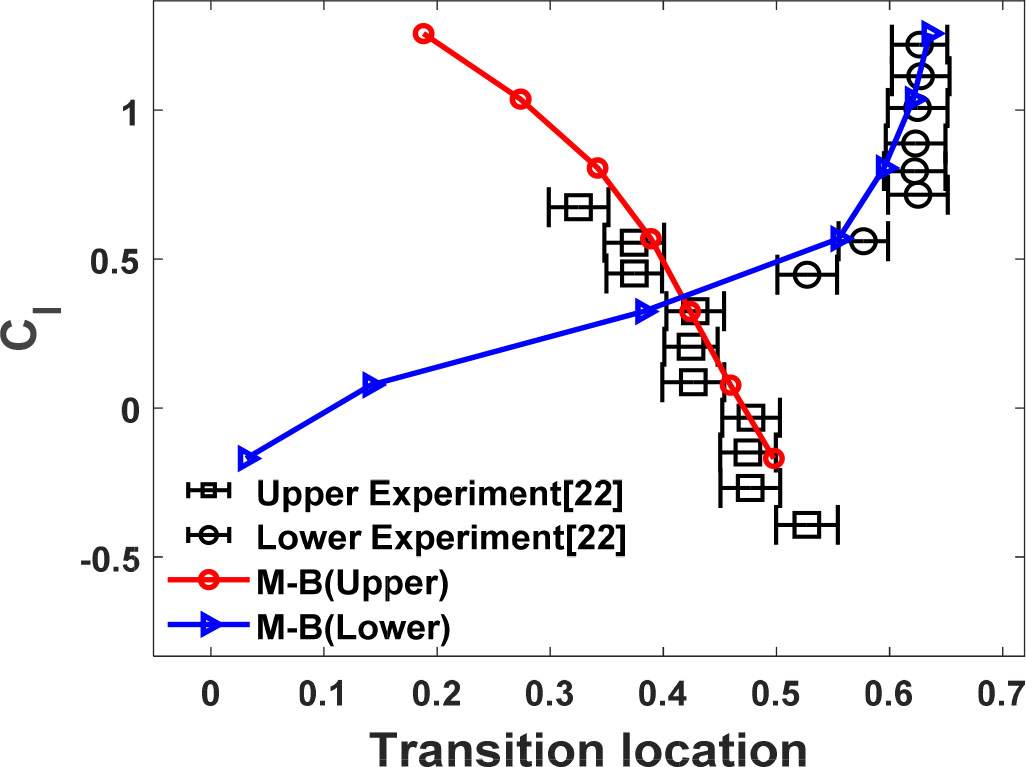
Fig. 6은 천이 위치를 실험값과 비교하였다. 받음각 -6°에서 6°까지 양력계수 범위는 –0.169에서 1.257까지 나타내고 있고 이는 양력계수 실험값과 잘 일치한다. 또한, 본 결과에서는 간헐성(𝛾)의 크기가 0.5 이상이 되는 지점을 천이 위치로 결정하고 익형 윗면과 아랫면의 천이 위치를 실험값과 비교하였다. 실험값은 양력계수에 따른 천이 위치를 오차 막대로 나타내었다. M-B 천이 모델의 천이 위치 결과는 실험값 범위 내에 위치함을 확인하였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F6.jpg

Fig. 6.

Comparison of transition onset locations for the NLF(1)-0416 airfoil with experimental data

3.1.2 Eppler387 익형

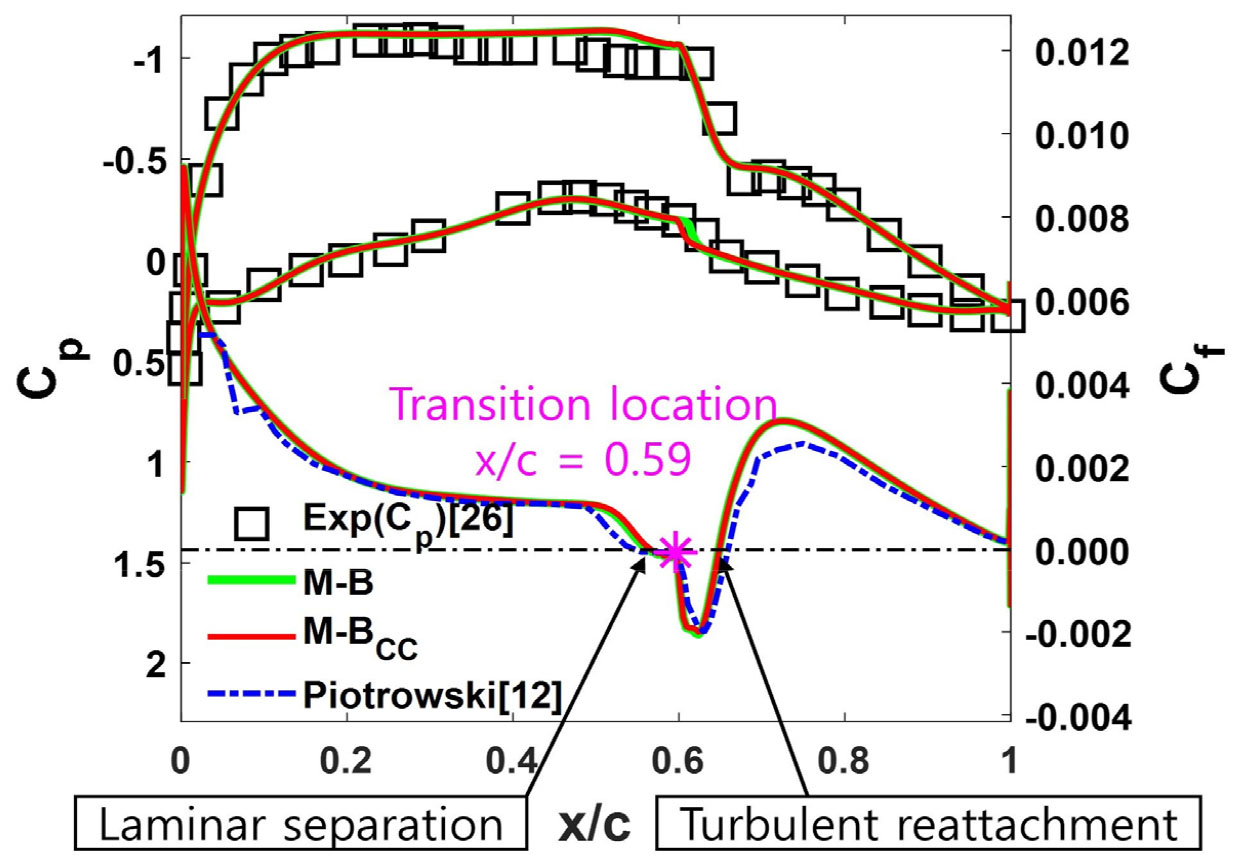
Eppler387 익형은 풍력 발전기 블레이드에 사용되는 익형으로 낮은 레이놀즈 수에서 얇은 층류 박리거품(Laminar Separation Bubble)을 예측할 수 있는 특징이 있다. 유동조건으로 마하수 0.1, 레이놀즈 수 $R e$ =2×10⁵와 자유류 난류강도 0.03%의 유동조건으로 미국 National Renewable Energy Laboratory(NREL)에서 풍동실험이 진행되었다[24].

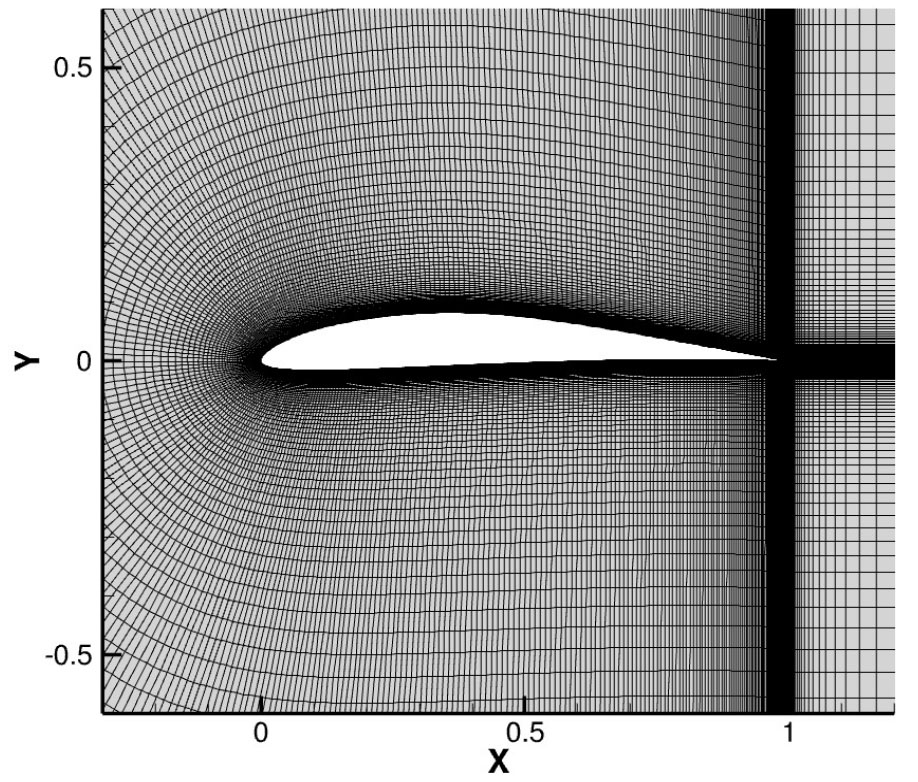
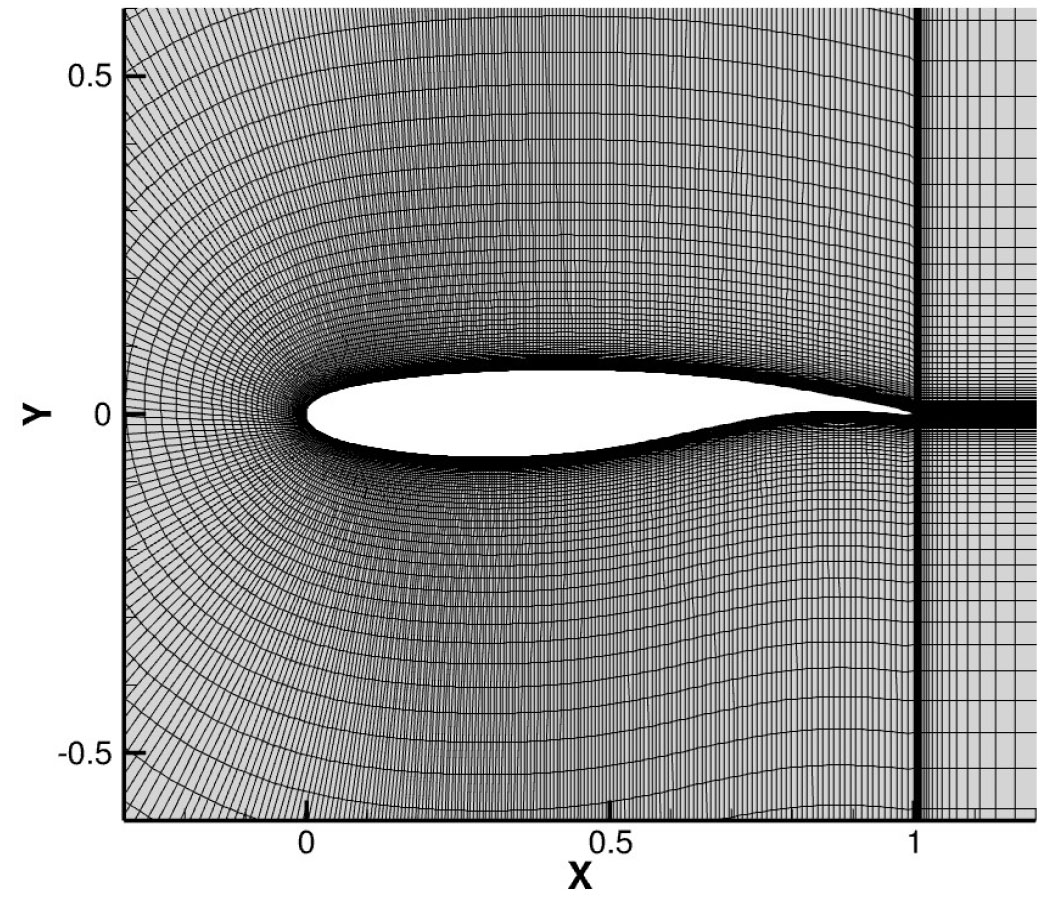
Eppler387 익형의 격자는 Fig. 7과 같이 C-type 정렬격자로 구성되었고 시위 길이의 100배에 해당되는 far-boundary 조건과 익형 표면은 no-slip 조건을 부여하였다. 익형 표면노드 수는 401개 $y^{+}$ =0.8에 의한 첫 번째 점성층은 시위 길이의 8.386×10^-6로 구성하여 받음각에 따른 층류 박리거품의 위치와 항력계수 비교를 통해 검증과 해석을 진행하였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F7.jpg

Fig. 7.

Eppler387 airfoil configuration composed of the Medium resolution grid

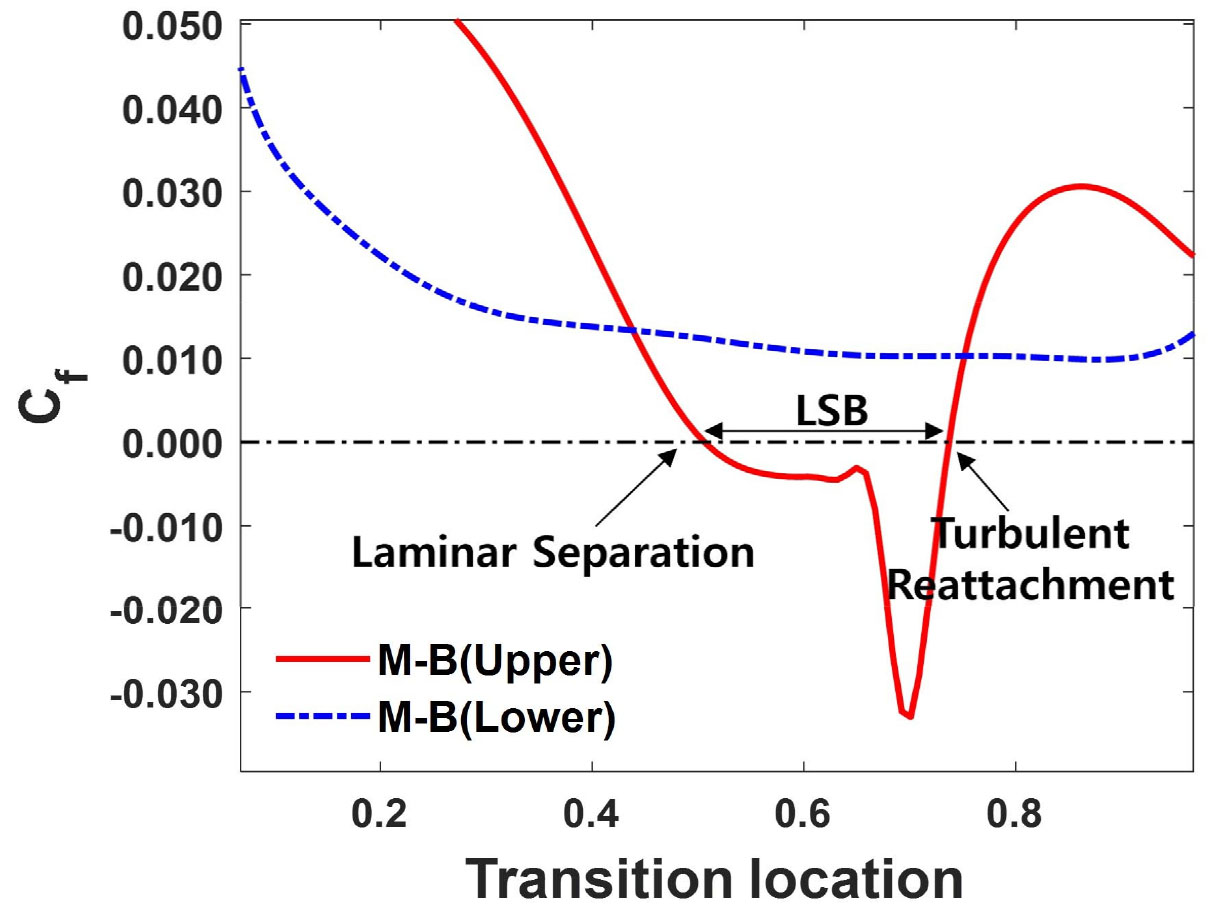
Fig. 8은 Eppler387 익형 받음각 0°의 표면 마찰계수 분포를 보인다. 윗면에서 층류 박리가 존재하는 영역에는 역방향 속도가 발생함에 따라 표면마찰계수는 음수 값을 갖게 된다. 천이과정 이후 난류 재부착이 발생하며 재부착 지점에서 양수 값을 갖게 된다. 천이 지점의 확인은 난류 간헐도(𝛾)가 0.5 이상이 되는 지점으로 확인한 결과 $x / c$ =0.6 부근에서 천이가 일어난 것을 확인하였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F8.jpg

Fig. 8.

Skin friction coefficient of Eppler387 airfoil at an angle of attack of 0 degrees

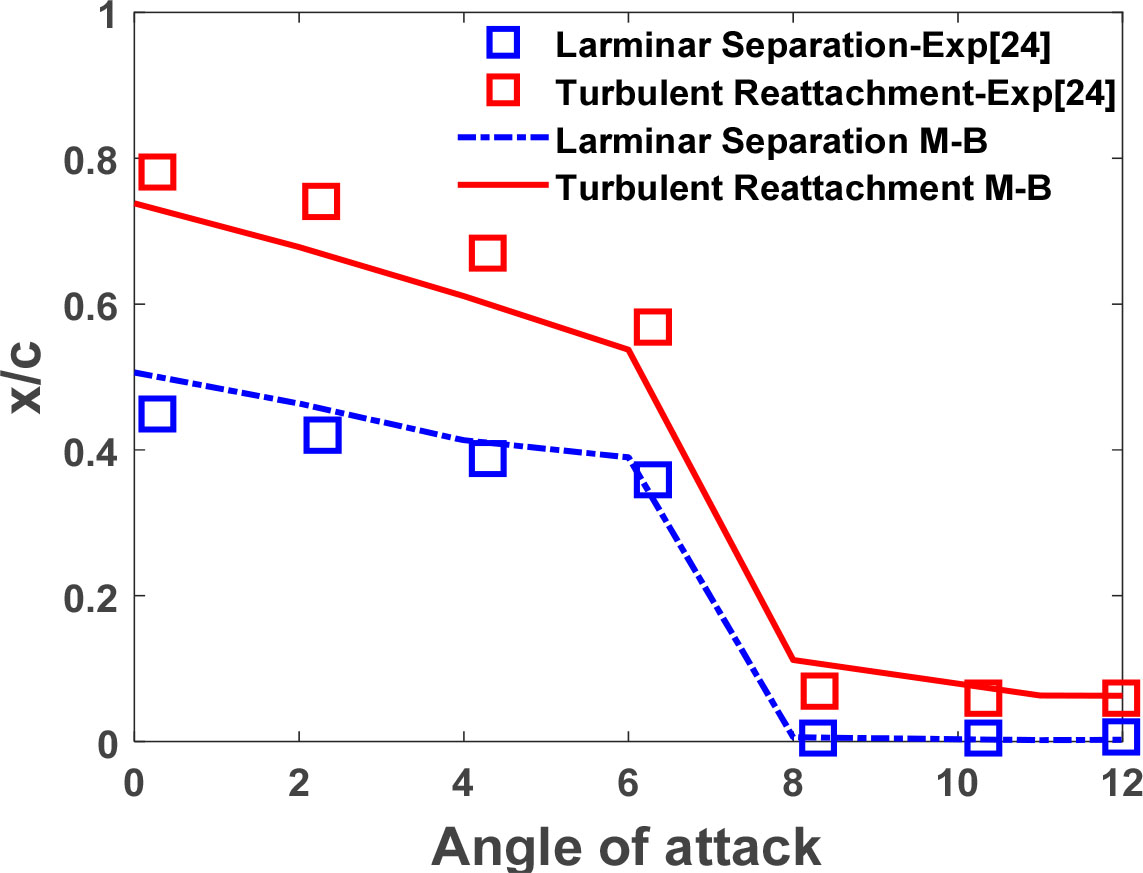
Fig. 9는 받음각에 따른 본 연구의 층류 박리 지점과 난류 재부착 지점을 실험값과 본 해석결과와 비교하였다. 받음각 0°의 $x / c$ =0.5지점에서 큰 박리거품을 예측하였고 받음각 6°까지 층류 박리와 난류 재부착 지점 위치가 상류 방향에 위치하는 결과가 실험값의 경향성과 일치하였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F9.jpg

Fig. 9.

Comparison of laminar separation and turbulent reattachment locations with experimental data on the upper surface of Eppler387 airfoil

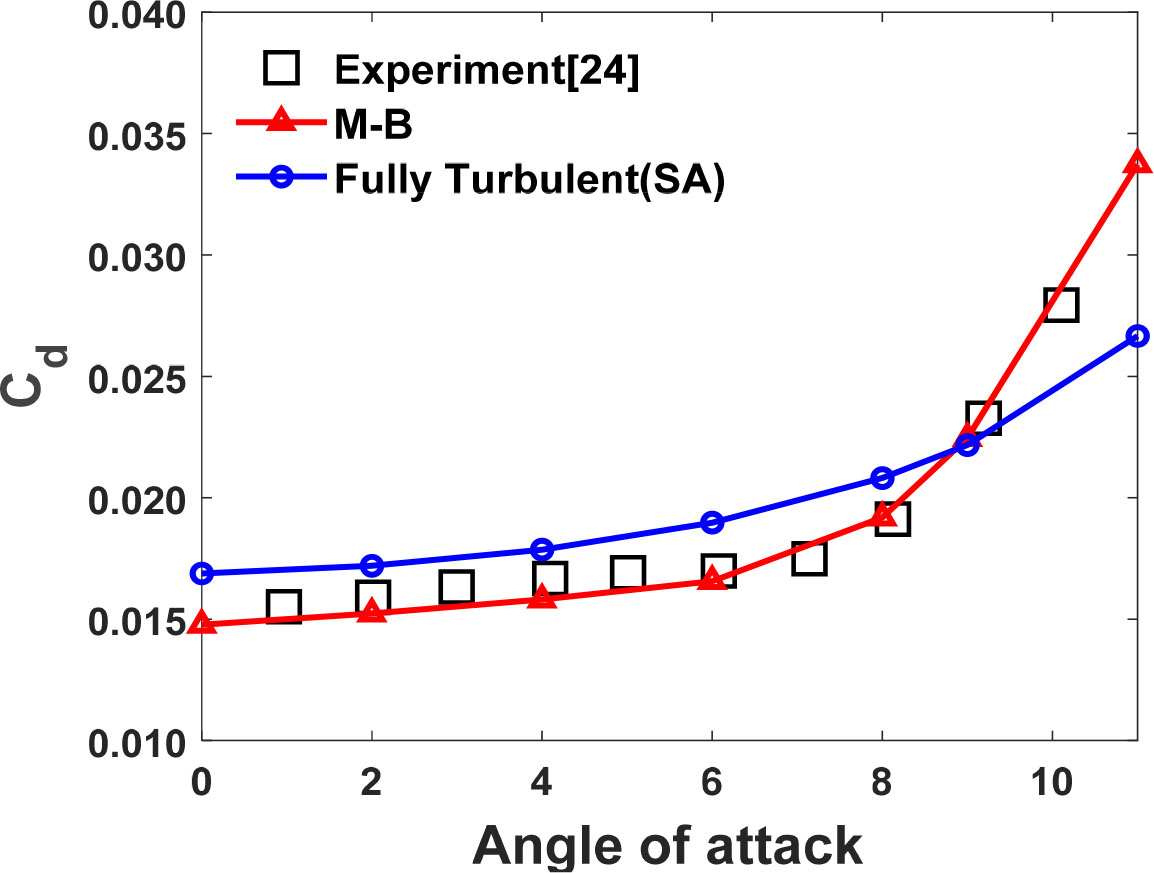
Fig. 10은 받음각에 따른 본 연구의 항력계수 결과로 받음각 0°에서 6°까지 완전 난류의 상황보다 익형 윗면의 중심 부근에서 층류 박리거품을 예측하는 M-B 천이 모델이 항력을 더 낮게 예측하였지만 받음각 9°부터 익형 앞전에서 예측한 박리거품의 영향으로 완전 난류의 상황보다 더 큰 항력을 예측하였고 이는 항력계수 실험값에 개선된 결과를 보여준다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F10.jpg

Fig. 10.

Comparison of drag coefficients for the Eppler387 airfoil between the experiment and predictions(SA turbulence and transition models)

3.2 천음속 익형 해석 및 검증

압축성 효과 보정식을 적용한 M-B CC(Compressibility Correction) 천이 모델에 대한 검증으로 천음속 영역, 특정 받음각에서 충격파를 동반하고 자연 천이를 일으키는 VA-2 익형과 박리 천이를 일으키는 CAST10-2 익형에 대한 해석 및 검증을 진행하였다.

3.2.1 VA-2 익형

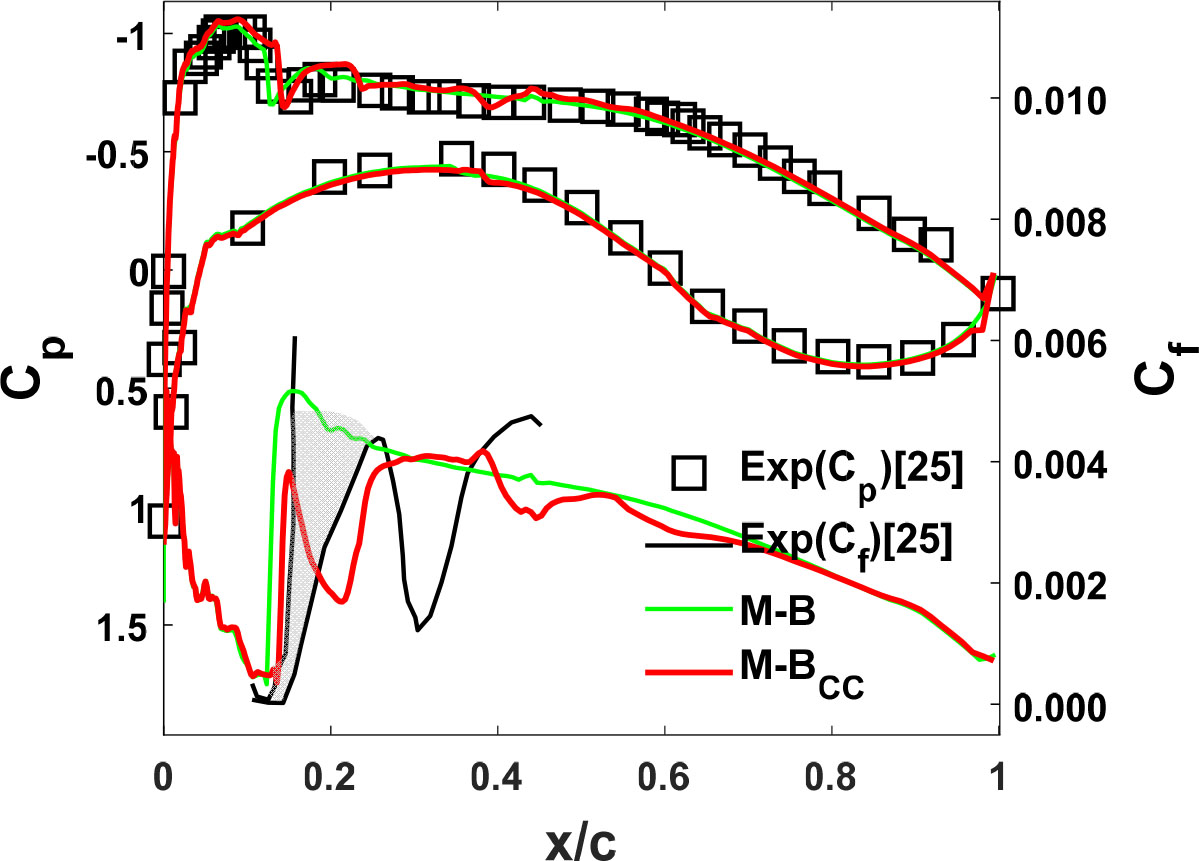
VA-2 익형은 마하수 0.71, 레이놀즈 수 $R e$ =10×10⁶과 난류강도 0.25%의 유동조건으로 Constanini 외 등[25]은 DNW-Transonic Wind Tunnel G¨ottingen(TWG)의 풍동실험을 수행하였다. 실험은 VA-2 익형 윗면에 대해 Global Luminescent Oil-Film Skin Friction field Estimation(GLOFSFE) 방법으로 표면 마찰계수를 측정하였고 불확실성에 의해 오차 범위가 존재한다. 또한, 표면 마찰계수 측정값을 각각 Schlichting, Blasius 경험식과 비교하여 천이 위치를 나타내었다. 따라서 그림에서 오차범위를 회색 음영 처리를 하였다(Figs. 12, 13, 14, 15).

VA-2 익형의 격자는 Table 2와 같이 구성하였다. Fig. 11과 같이 C-type 정렬격자로 구성되었고 시위 길이의 100배에 해당되는 경계에 far-boundary 조건과 익형의 표면은 no-slip 조건을 부여하였다. 익형 표면노드 수와 $y^{+}$ 에 의한 첫 번째 점성층은 Coarse, Medium, Fine 조밀성 단계의 격자에 따라 다르게 구성하였다.

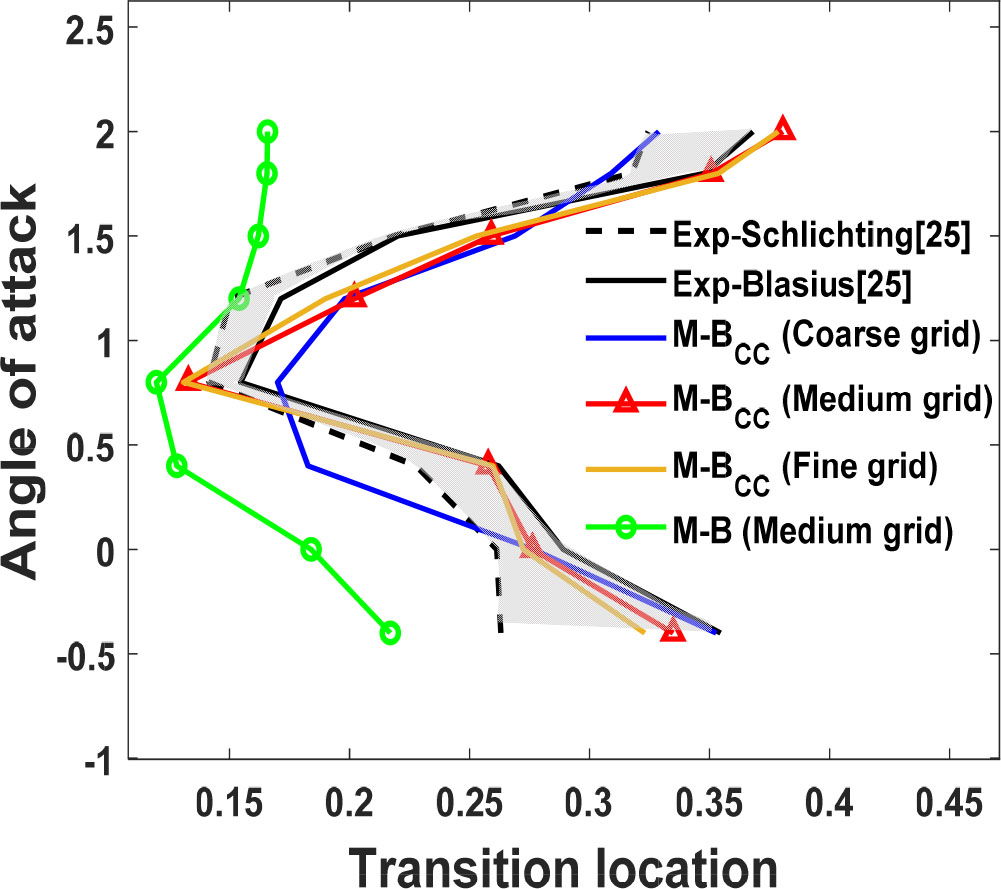
Fig. 12는 받음각에 따른 익형 윗면의 천이 위치를 나타낸 그래프로 격자 조밀성에 따라 실험값과 비교하였다. 본 연구의 천이 위치 결과는 익형의 윗면의 간헐성(intermittency) 크기가 0.5 이상이 되는 위치를 천이 위치로 결정하였다. M-B CC 천이 모델을 적용한 Coarse 격자는 실험값의 경향성에 벗어났고 Medium 격자의 결과는 Fine 격자의 결과와 유사함과 동시에 실험값의 경향성을 잘 보여준다. 따라서, 이후 결과는 Medium 조밀도 격자를 적용한 해석결과이다.

Table 2.

VA-2 airfoil C-grid dimensions

Grid level	Surface nodes	$y^{+}$	First wall-normal grid spacing
Coarse	201	1.2	3.328×10^-6
Medium	401	0.8	2.218×10^-6
Fine	801	0.4	1.109×10^-6

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F11.jpg

Fig. 11.

VA-2 airfoil configuration composed of the Medium resolution grid

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F12.jpg

Fig. 12.

Comparison of transition onset locations on the upper surface of the VA-2 airfoil with experiments

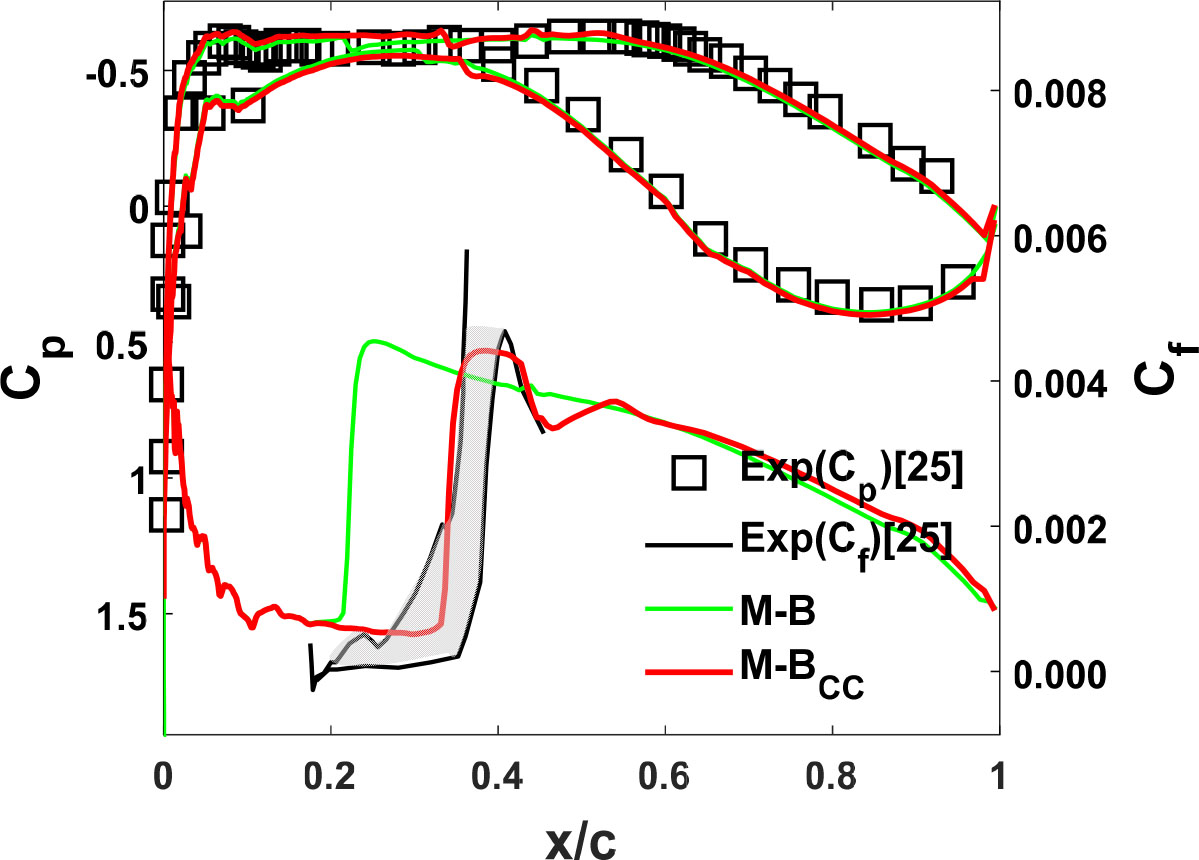
Fig. 13에서 받음각 –0.4°에 대한 본 연구의 결과로 익형 표면 압력계수 분포(위 그래프)와 윗면의 마찰계수(아래 그래프)를 실험값과 비교하였다. 윗면의 완만한 영 압력구배 조건에서 압축성 보정은 상대적으로 크게 이루어진다(Fig. 2 참조). 이는 M-B 천이 모델의 부정확한 천이 위치 예측 결과를 효과적으로 늦춰 실험값 오차 범위 안의 향상된 예측값을 보인다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F13.jpg

Fig. 13.

Comparison of surface pressure coefficient(top) and upper surface skin friction coefficient(bottom) with experimental data of the VA-2 airfoil at an angle of attack of –0.4 degrees

Fig. 14는 받음각 0.8°에 대한 본 연구의 결과로 윗면 마찰계수 그래프에서 M-B 천이 모델과 M-B CC 천이 모델의 천이 위치 차이가 크지 않다. 그 이유는 윗면의 역 압력구배가 증가하고 이는 압축성 효과 보정이 상대적으로 감소하여 본래 M-B 천이 모델에 가까워졌기 때문이다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F14.jpg

Fig. 14.

Comparison of surface pressure coefficient(top) and upper surface skin friction coefficient(bottom) with experimental data of the VA-2 airfoil at an angle of attack of 0.8 degrees

Fig. 15는 받음각 2.0°에 대한 본 연구의 결과로 받음각이 증가함에 따라 윗면의 유동 속도가 상대적으로 증가하게 되고 압력계수 분포 $x / c$ =0.43 부근에서 충격파가 발생한다. 충격파의 위치가 실험값과 일치하지 않지만 Piotrowski 외 등[12]의 압력계수 분포 결과 본 연구의 유사한 위치에서 충격파를 예측하였다. 충격파 형성으로 인해 상류에서 완만한 압력구배 형성되며, 압축성 보정 효과에 의해 경계층 천이가 늦춰진다. 이는 실험값에 더욱 근접한 결과이다. Fig. 15에서 경계층 천이는 충격파의 상류에 위치( $x / c$ =0.38)하므로 자연 천이에 의한 난류 경계층이 형성된 이후, 충격파가 발생함을 알 수 있다. 이처럼, 충격파를 동반한 자연 천이 상황에서도 예측 결과가 개선됨을 확인하였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F15.jpg

Fig. 15.

Comparison of surface pressure coefficient(top) and upper surface skin friction coefficient(bottom) with experimental data of the VA-2 airfoil at an angle of attack of 2.0 degrees

3.2.2 CAST10-2 익형

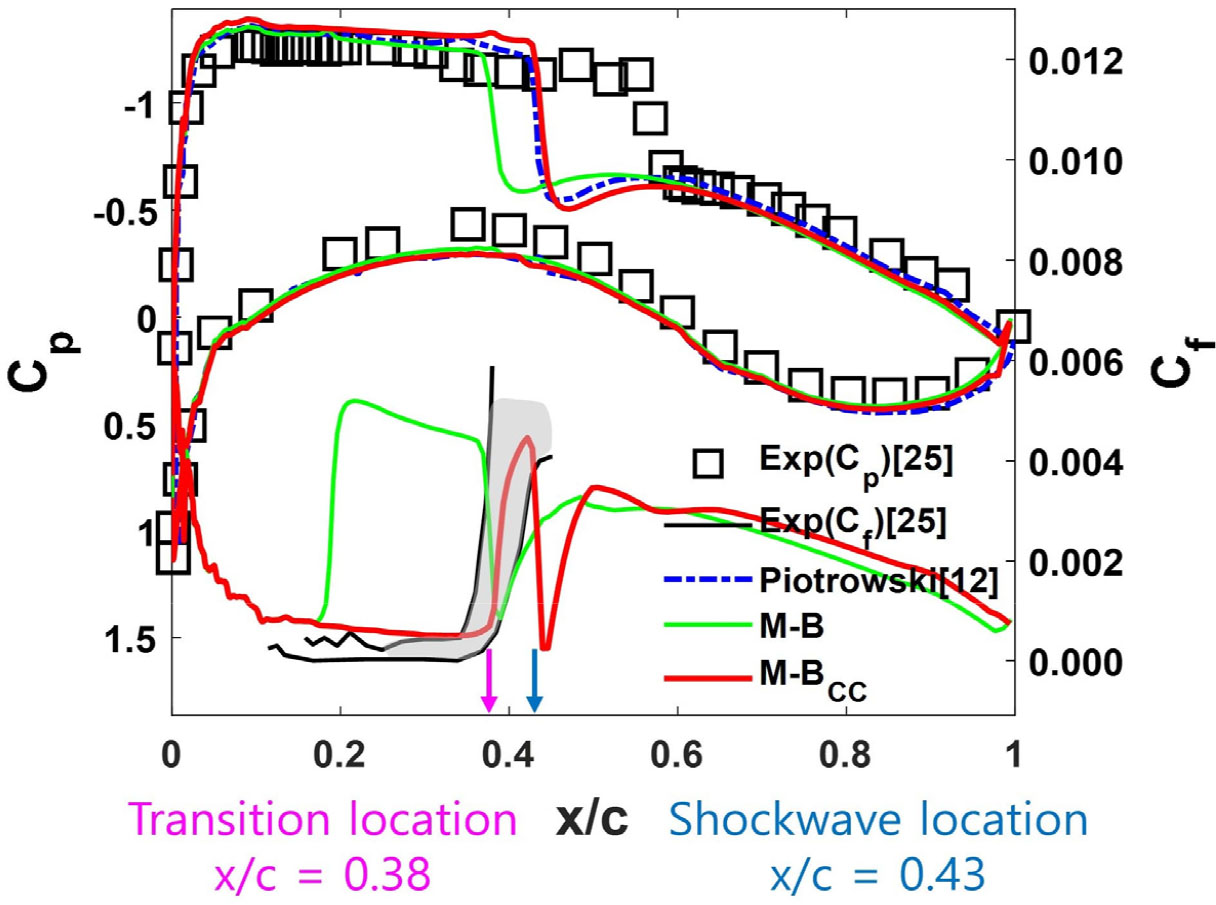
CAST10-2 익형은 마하수 0.74 레이놀즈 수 $R e$ 2×10⁶과 자유류 난류강도 0.25%의 유동조건으로 Hebler 외 등[26]은 DNW-TWG의 풍동실험을 진행하였다. CAST10-2 익형의 격자는 Fig. 16과 같이 O-type 정렬격자로 구성되었고 시위 길이의 100배에 해당되는 경계에 far-boundary 조건과 익형의 표면은 no-slip 조건을 부여하였다. 익형 표면노드 수는 401개 $y^{+}$ =0.8에 의한 첫 번째 점성층은 시위 길이의 9.889×10^-6로 구성하였다. 실험값이 존재하는 받음각 0.82°에 대한 해석을 진행하였고 익형 표면의 압력계수 분포를 비교하였고, 천이 위치 및 메커니즘을 판단하기 위해 마찰계수를 나타내었다. CAST10-2 익형의 경우 Eppler387과 같이 상대적으로 낮은 레이놀즈 수 조건에서 해석이 수행되었고, 윗면과 아랫면에서 층류 유동 박리가 일어난다.

Fig. 17은 CAST10-2 익형의 받음각 0.82°에 대한 해석결과로 $x / c$ =0.61 부근에서 충격파에 의한 압력의 변화를 확인하였다. 이것은 실험값과 일치한다. 또한, 윗면 마찰계수의 분포를 통해 박리거품의 위치를 확인할 수 있다. 경계층 내 난류 간헐도(𝛾)를 통해 $x / c$ =0.55 지점에서는 층류 박리가 $x / c$ =0.65 지점에서는 난류 재부착이 확인되었다. 이러한 결과는 Piotrowski 외 등[12]의 결과와 일치하는 것을 보여준다. 표면 마찰계수 및 압력계수의 분포에서 M-B 천이 모델과 M-B CC 천이 모델의 예측 결과가 일치함을 알 수 있다. 의도한 대로, 압축성 효과가 오직 T-S 불안정성에 의한 천이 메커니즘에 영향을 주며 유동 박리 천이에 영향을 주지 않음을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F16.jpg

Fig. 16.

CAST10-2 airfoil configuration and O-type structured grid

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F17.jpg

Fig. 17.

Comparison of surface pressure coefficient(top) and upper surface skin friction coefficient(bottom) with experimental data of the CAST10-2 airfoil at an angle of attack of 0.82 degrees

3.2.3 NASA CRM-NLF 해석

NASA Langley Research Center의 CRM-NLF는 천음속 영역에서 운항되는 차세대 민항공기의 연구 목적으로 새로운 NLF 기법 중 하나인 Crossflow Attenuated Natural Laminar Flow(CATNLF)를 적용하여 설계된 형상이다. CATNLF 기법은 천음속 영역에서 지배적인 T-S와 crossflow 중 crossflow에 의한 천이를 제한하는 방법이다. Crossflow는 주로 후퇴익 형상에서 발생하는 유선의 급격한 변화로 주 유동 방향으로 진행될 때와 다르게 빠른 천이를 유도하는 원인이 된다[27].

천음속 풍동실험 데이터는 동체와 날개 밑면에 강제 난류를 적용하였으며 압력계수 분포와 날개 윗면의 천이 위치등을 측정하였다. 유동 조건으로 받음각에 따라 Table 3과 같이 주어졌고 레이놀즈 수는 Mean Aerodynamic Chord(MAC) 기반으로 정의되었다[27].

Table 3.

The flow condition of CRM-NLF

Angle of attack	Mach number	Reynolds number(MAC)
1.44848°	0.856489	14.97197×10⁶
1.98031°	0.856491	14.94591×10⁶
2.46141°	0.856051	14.90909×10⁶
2.93787°	0.855801	14.85308×10⁶

본 해석자에 적용 가능한 crossflow 천이 모델[19]의 경우, 상대적으로 높은 표면 거칠기에서 검증되었으므로, 상대적으로 낮은 표면 거칠기를 갖는 CRM-NLF 해석에는 사용하지 않았다. 또한, 동일한 유동 조건에서 선행 연구들[14,27,28]을 통해 crossflow에 의한 불안정성이 경계층 천이의 주된 메커니즘이 아님이 검증되었다.

CRM-NLF half-model 격자는 2021 AIAA Transtion Modeling and Prediction Workshop에서 제안된 격자 지침서에 규정된 정보를 이용하였다[29]. 표면 격자로 Fig. 18과 같이 날개는 정렬격자를 적용하였고 동체는 비정렬격자를 적용하였다. 날개의 표면 격자는 스팬 방향으로 326개, 시위 방향으로 240개의 격자점으로 구성되었다. 동체-날개 표면은 no-slip 조건을 적용하였으며, Fig. 19와 같이 첫 번째 점성층은 유동 조건의 $y^{+}$ =2/3을 적용하고, 표면 격자의 수직한 방향으로 1.15 배의 성장률을 적용하였다.

동체-날개의 경계층 영역을 포함한 strand-type volume 격자는 Stretched Cartesian 격자로 구성된 background 영역과 중첩된다. Background 영역의 동체와 연결된 경계면은 half-model 해석을 위해 symmetric 경계 조건을 부여하였으며, 나머지 경계면은 항공기 날개 semi-span의 100배 거리에 위치하며 far-field 경계 조건을 적용하였다. 동체-날개 영역과 background 영역 사이에 Cartesian 격자를 이용한 nested 영역을 중첩하였다. Jung 외 등[30]에서 동일 격자에 대한 격자 조밀성에 대한 연구가 수행되었으며, 본 연구에서는 Medium 격자에 해당하는 격자를 사용하였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F18.jpg

Fig. 18.

Surface meshes and applied boundary condition for the CRM-NLF half-model simulations

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F19.jpg

Fig. 19.

Wing strand volume grid and overset nested mesh for the CRM-NLF half-model simulations

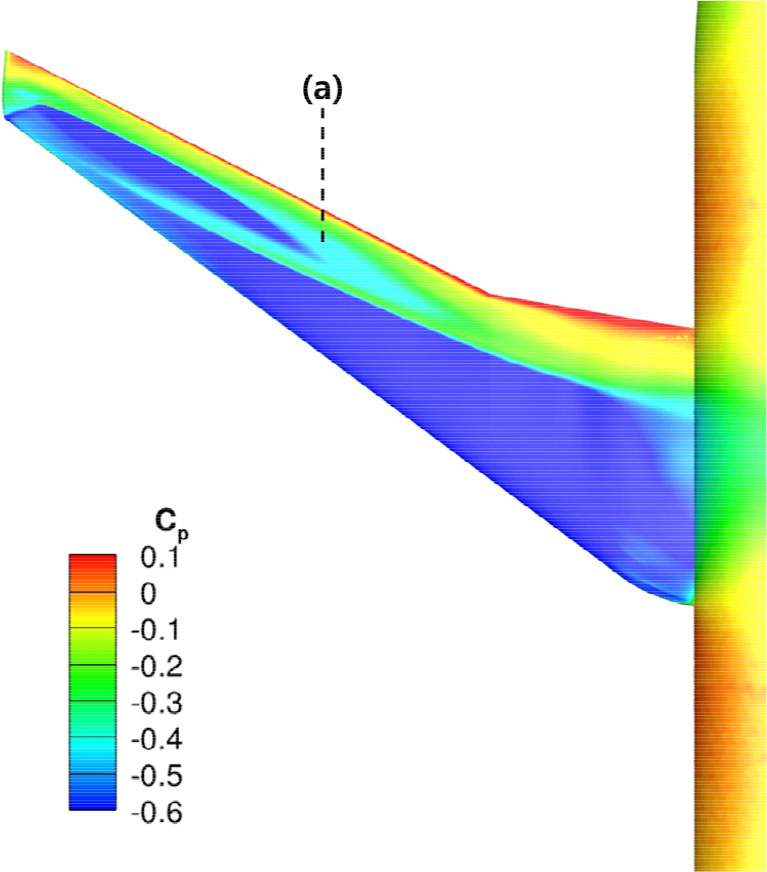
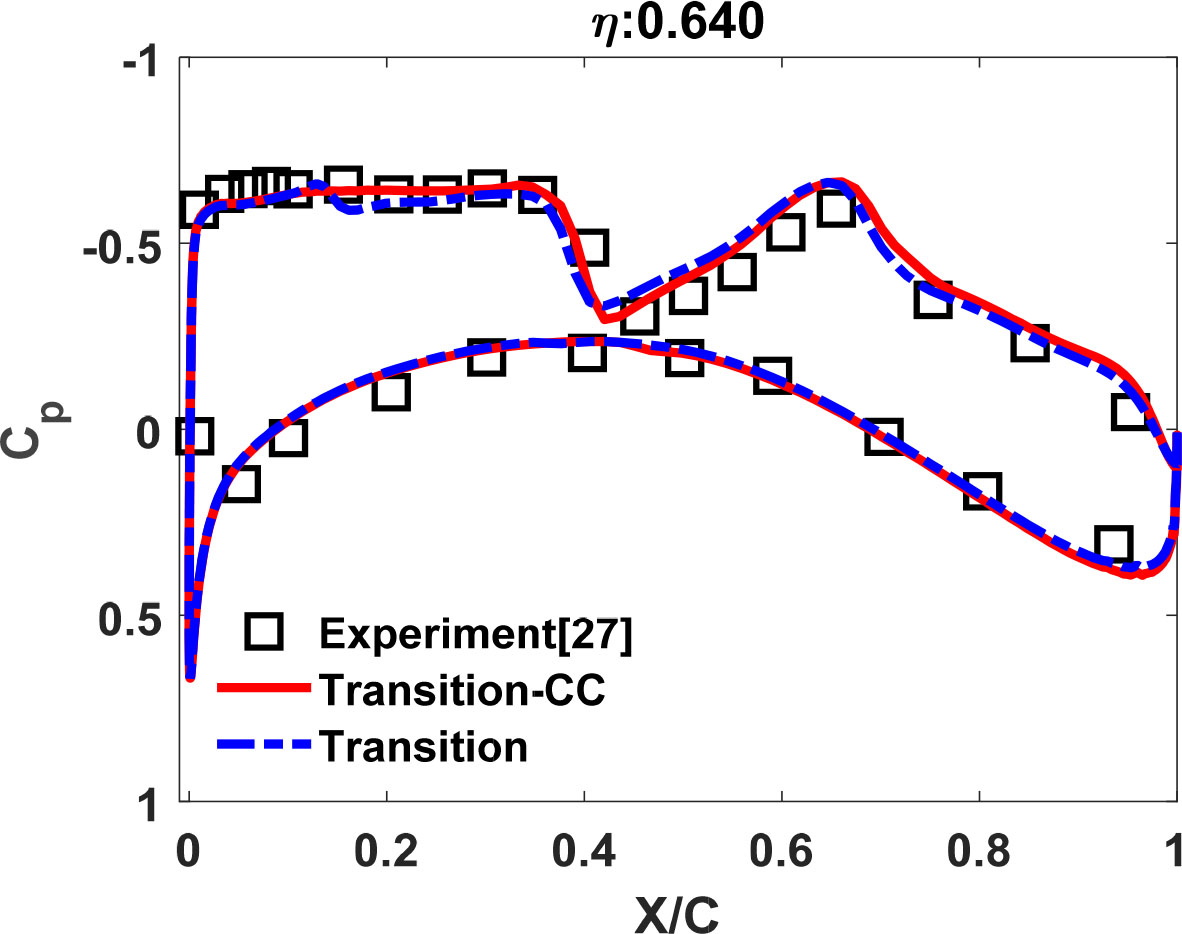
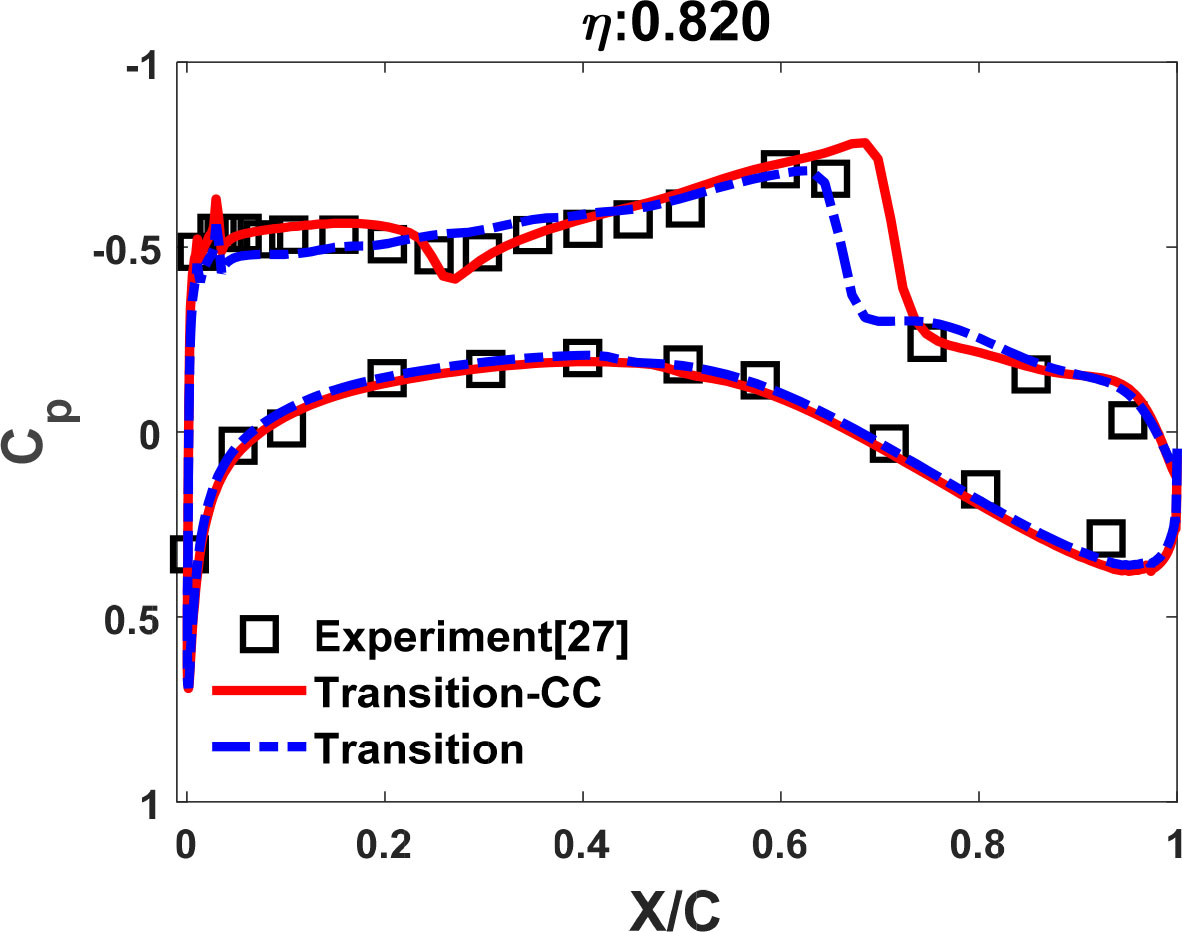
Fig. 20은 M-B CC 천이 모델을 적용한 받음각 2.94°윗면 날개에 대한 압력분포도이다. 스팬 방향으로 (a)구간 부터 부근에 뚜렷한 이중 충격파를 예측하였다. Fig. 21은 날개 뿌리에서 스팬 방향으로 64%(𝜂=0.64) 구간을 Fig. 22는 동일하게 84%(𝜂=0.82) 구간에 해당되는 날개 단면의 표면 압력 분포를 나타낸 그래프이다. 이는 M-B 천이 모델, M-B CC 천이 모델과 실험값을 함께 비교하였다. 𝜂=0.64 구간에서 M-B 천이 모델, M-B CC 천이 모델 모두 실험값과 동일한 결과를 얻었으며 시위 방향의 0.35( $x / c$ )에서 첫 번째 충격파와 0.65( $x / c$ )에 두 번째 충격파를 예측하였다. 𝜂=0.82 구간에서는 두 모델 모두 실험값과 유사한 결과를 얻었지만 M-B CC 천이 모델은 0.25( $x / c$ )에 발생하는 약한 충격파를 실험값의 경향성을 예측하였다. 하지만 두 번째 충격파에서 M-B CC 천이 모델이 0.68( $x / c$ )에서 충격파를 예측하므로 실험값보다 늦춰진 것을 알 수 있다. 이는 압축성 효과 보정식이 천이 위치를 지연함으로써 충격파의 위치가 지연되었기 때문이다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F20.jpg

Fig. 20.

Surface pressure coefficient contour on the wing upper surface of the CRM-NLF at an angle of attack of 1.98031 degrees

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F21.jpg

Fig. 21.

Sectional(𝜂=0.64) wing surface pressure distribution at an angle of attack of 1.98031 degrees of the CRM-NLF configuration

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F22.jpg

Fig. 22.

Sectional(𝜂=0.82) wing surface pressure distribution at an angle of attack of 1.98031 degrees of the CRM-NLF configuration

Fig. 23은 모든 받음각에 대한 본 연구의 M-B CC 천이 모델의 결과로 날개 윗면에서 turbulence index[31] 분포를 보인다. 천이 위치의 판별은 turbulence index를 사용하였다. turbulence index는 1에 가까울수록 난류 영역을 의미하고 0에 가까울수록 층류 영역을 의미한다. 본 연구에서 예측된 천이 위치는 실험값[27] 뿐만 아니라, 압축성 효과가 배제된 M-B 천이 모델[30]과 $e^{N}$ 모델[28]을 통해 예측된 선행연구의 해석결과와 비교되었다. 이중, $e^{N}$ 모델을 적용한 Fischer 외 등[28]에서 CRM-NLF를 구성한 표면 격자는 스팬 방향으로 348개, 시위 방향으로 240개의 격자로 구성되었고 첫 번째 점성층은 $y^{+}$ =0.3으로 구성하였다. 본 연구 격자와 표면격자 구성은 거의 일치하나 $y^{+}$ 값은 2배 가까이 작다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290202/images/jkscfe_2024_292_013_F23.jpg

Fig. 23.

Comparison of transition onset locations on the upper surface of the CRM-NLF wing: Experiment[27] and other predictions[28,30]

전반적으로, M-B 천이 모델을 적용한 선행연구[30]의 결과는 실험값에 비해 상당한 상류에서 천이를 예측하였음을 알 수 있다. 이러한 경향은 M-B 천이 모델뿐만 아니라 $γ - {\tilde{R e}}_{θ t}$ 등의 경험적 상관관계식 기반의 천이 모델에서 공통적으로 나타난다[11]. 하지만, 압축성 효과를 고려한 M-B CC 천이 모델의 예측 결과는 천이 위치를 효과적으로 지연시켰고, 이는 실험값에 비교할 때 상당한 개선을 보이고 있음을 알 수 있다.

구체적으로, 받음각 1.44°에서 뒷전 후퇴각이 급변하는 break 영역에서 날개 끝까지 M-B CC 천이 모델에서 예측한 천이 위치는 실험값과 상당히 유사하며, 선형 안정성 기반의 $e^{N}$ 모델과 유사한 정확도를 보여준다. 하지만 M-B CC 천이 모델 결과는 날개 뿌리에서 break 영역까지 천이 위치를 상류 영역에서 일찍 예측하였다.

받음각 1.98°에서 날개 끝단을 제외한 영역에서 천이 위치가 앞당겨졌으며 이는 실험값과 동일하게 나타난다. 날개 뿌리를 제외한 모든 영역에서 M-B CC 천이 모델의 예측 결과는 실험값과 상당히 유사하였으며, $e^{N}$ 모델의 결과와도 유사함을 알 수 있다.

받음각 2.46°에서 날개 끝단의 층류 영역이 감소하였으며, (b) 구간부터 (c)구간에서 천이가 앞당겨 졌다. M-B CC 모델의 경우 break 부근부터 날개 끝까지 실험값과 유사한 결과를 보여주었다. 하지만, $e^{N}$ 모델의 결과와 동일하게 (b) 구간부터 (c)구간까지 층류 영역을 더 크게 예측하였다.

받음각 2.94°에서 M-B CC 천이 모델 결과는 국부적으로 실험값와 차이가 존재하였다. 예를 들어, break 영역에서 (d)구간까지 실험값에 비해 천이 지점을 일찍 예측하였고, (e)구간에서 break 까지는 실험값에 비해 늦게 예측하였다. $e^{N}$ 모델의 결과 또한 본 해석결과와 동일한 경향성을 갖고 실험값을 정확히 예측하는데 한계가 있음을 알 수 있다.

모든 받음각에서 본 예측 결과는 날개 뿌리에서 부정확한 천이 위치를 예측하였으며, 이를 개선하기 위한 후속 연구가 필요하다.

4. 결 론

본 연구에서는 RANS 기반의 Medida-Baeder 경계층 천이 모델에 압축성 효과 보정식을 적용하여 천음속 유동 익형과 NASA CRM-NLF에 대한 해석을 진행하였다. 우선, 아음속 영역에서의 다양한 천이 메커니즘의 예측 정확도 검증을 수행하였다. 자연 천이가 발생하는 NLF(1)-0416 와 박리 천이가 발생하는 Eppler 387 익형에 대한 해석을 수행하였고, 실험에 의해 확인된 천이 메커니즘을 예측하였다. 또한, 받음각에 따른 천이 위치 및 공력계수 값이 실험값과 일치함을 확인하였다.

이후, 압축성 효과 보정식이 적용된 Medida-Baeder 천이 모델은 천음속 유동 상황에서 Tollmien-Schlichting 천이 원리에 따라 보정식의 타당함을 보여줬다. 받음각 –0.4°에서 VA-2 익형 윗면에 발생한 순 압력구배 조건에서, 기존의 Medida-Baeder 천이 모델은 천이 위치를 일찍 예측하였지만 천이 위치를 늦추는 압축성 보정 효과로 인해 실험값에 근접하였다. 반면, 받음각이 증가한 0.8°에서는 익형 윗면의 역 압력구배로 인해 압축성 보정 효과가 감소하였고, 기존 Medida-Bader 천이 모델의 예측 결과와 유사하였다. 받음각 2.0°의 경우 익형 윗면에서 충격파가 발생하였고, 상류의 완만한 압력구배 조건에서 천이 위치가 충격파 직전까지 늦춰짐을 잘 예측하였다. CAST10-2 익형의 경우 낮은 레이놀즈 수 조건에서 발생한 층류 박리거품에 의한 박리 천이를 유도하게 된다. 본 압축성 보정은 박리 천이에 영향을 주지 않고, 기존 Medida-Baeder 천이 모델로 수렴한 것을 확인하였다.

최종적으로, 천음속 유동 조건에서 다양한 실험데이터가 존재하는 NASA CRM-NLF 삼차원 형상을 통해 개선된 결과를 확인하였다. 해석이 수행된 모든 받음각에서 압축성 보정은 효과적으로 천이 위치를 늦추었으며, 이는 실험값에 근접하였다. 또한, 개선된 결과는 타 연구자의 $e^{N}$ 모델에 기반한 해석결과와 비교하였으며, 유사한 정확도를 보였다. 반면에, 상대적으로 높은 받음각인 2.46°, 2.94°에서 날개 뿌리부터 break 구간에서 실험값에 비해 층류 경계층 영역을 과도하게 예측하였다. 후속 연구를 통해 표면 거칠기를 고려할 수 있는 Langtry 외 등[7]의 crossflow 천이 모델을 적용하여, 개선될 수 있는지 연구할 계획이다. 또한, 본 연구에 사용된 압축성 효과 보정식은 경계층 마하수 1.1 이하의 외부유동에서 유효함에 따라, 범용성을 넓힐 수 있는 후속 연구가 제안된다.

Acknowledgements

이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음. 또한, 이 연구는 4단계 BK21 드론 신산업 혁신인재 교육연구단 사업으로 지원되었음.

References

2000, Pope, S., "Turbulent Flows," Cambridge University Press, UK.

1995, Wilson, R.A.L. and Jones, R.I., "Project Design Studies on Aircraft Employing Natural and Assisted Laminar Flow Technologies," SAE Transactions, Vol.104, pp.1571-1582.

2010, Allison, E., Kroo, I., Suziki, Y. and Martins-Ricas, H., "Aircraft conceptual design with natural laminar flow," In: 27^th International Congress of the Aeronautical Sciences(ICAS).

2009, Langtry, R.B. and Menter, F.R., "Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes," AIAA J., Vol.47, No.12, pp.2894-2906

10.2514/1.42362

2018, Han, Z.H., Chen, J., Zhang, K.S., Xu, Z.M., Zhu, Z. and Song, W.P., "Aerodynamic Shape Optimization of Natural-Laminar-Flow Wing Using Surrogate-Based Approach," AIAA J., Vol.56, No.7, pp.2579-2593.

10.2514/1.J056661

2023, Thurman, C., David, D.B. and Simmons, B.M., "Comparison of Prediction Modeling Methodologies for Aeroacoustic Characterization of Hovering sUAS Rotors," In: AIAA SCITECH 2023 Forum.

10.2514/6.2023-0027

2015, Langtry, R.B., Sengupta, K., Yeh, D.T. and Dorgan, A.J., "Extending the Gamma-Rethetat Correlation basedTransition Model for Crossflow Effects (Invited)," In: 45^th AIAA Fluid Dynamics Conference.

2012, Dassler, P., Kozulovic, D. and Fiala, A., "An Approach for Modelling the Roughness-Induced Boundary Layer Transition Using Transport Equations," In: 6^th European Congress on Computational Methods in Applied Sciences and Engineering.

2011, Arnal, D. and Vermeersch, O., "Compressibility effects on laminarturbulent boundary layer transition," Int. J. Eng. Syst. Model. Simul., Vol.3, No.1-22, pp.26-35.

10.1504/IJESMS.2011.038747

1988, Arnal, D., "Transition prediction in transonic flows, Symposium Transsonicum III," IUTAM, Springer, Berlin, Germany.

2022, Marie, D., "1st AIAA CFD Transition Modeling and Prediction Workshop: OVERFLOW Results for the SST and Langtry-MenterModels," In: AIAA SCITECH 2022 Forum.

2022, Piotrowski, M., and Zingg, D., "Compressibility Corrections to Extend a Smooth Local Correlation-Based Transition Model to Transonic Flows." The Aeronaut. J., Vol.127, No.127, pp.1141-1170.

10.1017/aer.2022.105

2014, Perraud, J,, Deniau, H. and Casalis, G., "Overview of transition prediction tools in the elsA software," In: 2014 CCOMAS.

2022, Venkatachari, B.S., Paredes, P., Choudhari, M.M., Li, F. and Chang, C.L., "Transition Analysis for the CRM-NLF Wind Tunnel Configuration using Transport Equation Models and Linear Stability Correlations," In: AIAA SCITECH 2022 Forum.

10.2514/6.2022-154235566903PMC9104345

2018, Qiao, L., Bai, J.Q., Xu, J.K., Xu, J.L. and Zhang, Y., "Modeling of Supersonic/Hypersonic Boundary Layer Transition Using a Single-Point Approach," Int. J. Nonlinear Sci. Numer. Simul., Vol.19, No.3-4, pp. 263-274.

10.1515/ijnsns-2017-0011

2023, Sturdza, P., "An Aerodynamic Design Method for Supersonic Natural Laminar Flow Aircraft," Ph.D. Thesis, Stanford University, California, USA

2011, Arnal, D., Houdeville, R., Seraudie, A., and Vermeersch, O., "Overview of laminar-turbulent transition investigations at ONERA Toulouse," In: 41^th AIAA Fluid Dynamics Conference and Exhibit.

2014, Medida, S., "Correlation-based Transition Modeling for External Aerodynamic Flows," PhD. Thesis, University of Maryland, College Park, USA.

2019, Jung, Y.S. and Baeder. J., "𝛾-𝑅𝑒𝜃𝑡-Spalart-Allmaras with Crossflow Transition Model Using Hamiltonian-Strand Approach," J. Aircr., Vol.56, No.3, pp.1040-1055.

2023, Jung, Y.S., Lee, B. and Baeder, J., "Prediction of Coaxial Rotor Hub Flow Using Mercury Framework," In: 75^th Journal of the American Helicopter Society Forum.

2017, Jung, Y.S., Govindarajan, B. and Baeder, J., "Turbulent and Unsteady Flows on Unstructured Line-Based Hamiltonian Paths and Strands Grids," AIAA J., Vol.55, No.6, pp.1986-2001.

10.2514/1.J055141

1981, Somers, D.M., "Design and experimental results for a natural-laminar-flow airfoil for general aviation applications," NASA Technical Publication.

2018, Coder, J.G., "Standard test cases for transition model verification and validation in computational fluid dynamics," In: 2018 AIAA Aerospace Sciences Meeting.

10.2514/6.2018-0029PMC6624839

2004, Selig, M.S. and McGranahan, B.D., "Wind tunnel aerodynamic tests of six airfoils for use on small wind turbines," J. Sol. Energy Eng., Vol.126, pp.986-1001.

10.1115/1.1793208

2021, Costantini, M., Lee, T., Nonomura, T., Asai, K. and Klein, C., "Feasibility of skin-friction field measurements in a transonic wind tunnel using a global luminescent oil film," Exp. Fluids, Vol.62, No.1, p.21.

10.1007/s00348-020-03109-z

2013, Hebler, A., Schojda, L. and Mai, H., "Experimental investigation of the aeroelastic behavior of a laminar airfoil in transonic flow," In: 2013 IFASD.

2019, Lynde, M.N., Campbell, R.L., Rivers, M.B., Viken, S.A., Chan, D.T., Watkins, N.A. and Goodliff, S.L., "Preliminary results from an experimental assessment of a natural laminar flow design method," In: 2019 AIAA Aerospace Sciences Meeting.

10.2514/6.2019-2298

2021, Fischer, J.S., Soemarwoto, B.I. and Edwin, T.A. van der Weide., "Automatic Transition Prediction in a Navier-Stokes Solver Using Linear Stability Theory," AIAA J., Vol.59, No.7, pp.2409-2426.

10.2514/1.J059910

General Information on the Wind Tunnel Data from the CRM-NLF test (website : https://commonresearch model.larc.nasa.gov/)

2021, Jung, Y.S., Lee, B.S. and Baeder, J., "Validation of SA-𝛾-𝑅𝑒𝜃𝑡 and SA-𝛾 Turbulence/Transition Models," In: 1^st AIAA Transition Modeling and Prediction Workshop.

1992, Spalart, P.R. and Allmaras, S.R., "A One-Equation Turbulence Model forAerodyanmics Flows," In: 30^th AIAA Sciences Meetingand Exhibit.

Journal of Computational Fluids Engineering ISSN:1598-6071(Print) 3022-6252(Online) 한국전산유체공학회지

Preview

BOUNDARY LAYER TRANSITION MODEL WITH COMPRESSIBILITY CORRECTION FOR TRANSONIC FLOW SIMULATIONS

ABSTRACT

MAIN

Fig. 1.

Transition onset momentum thickness Reynolds number as a function of boundary layer Mach number at zero pressure gradient

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 2.

The compressibility correction as a function of boundary layer Mach number and pressure gradient

(7)

(8)

(9)

(10)

(11)

(12)

(13)

Table 1.

NLF(1)-0416 airfoil C-grid dimensions

Fig. 3.

NLF(1)-0416 airfoil configuration composed of the Medium resolution grid

Fig. 4.

Skin friction coefficient of NLF(1)-0416 airfoil at an angle of attack of 0 degrees

Fig. 5.

Comparison of drag coefficients for the NLF(1)-0416 airfoil between the experiment and predictions(SA turbulence and transition models)

Fig. 6.

Comparison of transition onset locations for the NLF(1)-0416 airfoil with experimental data

Fig. 7.

Eppler387 airfoil configuration composed of the Medium resolution grid

Fig. 8.

Skin friction coefficient of Eppler387 airfoil at an angle of attack of 0 degrees

Fig. 9.

Comparison of laminar separation and turbulent reattachment locations with experimental data on the upper surface of Eppler387 airfoil

Fig. 10.

Comparison of drag coefficients for the Eppler387 airfoil between the experiment and predictions(SA turbulence and transition models)

Table 2.

VA-2 airfoil C-grid dimensions

Fig. 11.

VA-2 airfoil configuration composed of the Medium resolution grid

Fig. 12.

Comparison of transition onset locations on the upper surface of the VA-2 airfoil with experiments

Fig. 13.

Comparison of surface pressure coefficient(top) and upper surface skin friction coefficient(bottom) with experimental data of the VA-2 airfoil at an angle of attack of –0.4 degrees

Fig. 14.

Comparison of surface pressure coefficient(top) and upper surface skin friction coefficient(bottom) with experimental data of the VA-2 airfoil at an angle of attack of 0.8 degrees

Fig. 15.

Comparison of surface pressure coefficient(top) and upper surface skin friction coefficient(bottom) with experimental data of the VA-2 airfoil at an angle of attack of 2.0 degrees

Fig. 16.

CAST10-2 airfoil configuration and O-type structured grid

Fig. 17.

Comparison of surface pressure coefficient(top) and upper surface skin friction coefficient(bottom) with experimental data of the CAST10-2 airfoil at an angle of attack of 0.82 degrees

Table 3.

The flow condition of CRM-NLF

Fig. 18.

Surface meshes and applied boundary condition for the CRM-NLF half-model simulations

Fig. 19.

Wing strand volume grid and overset nested mesh for the CRM-NLF half-model simulations

Fig. 20.

Surface pressure coefficient contour on the wing upper surface of the CRM-NLF at an angle of attack of 1.98031 degrees

Fig. 21.

Sectional(𝜂=0.64) wing surface pressure distribution at an angle of attack of 1.98031 degrees of the CRM-NLF configuration

Fig. 22.

Sectional(𝜂=0.82) wing surface pressure distribution at an angle of attack of 1.98031 degrees of the CRM-NLF configuration

Fig. 23.

Comparison of transition onset locations on the upper surface of the CRM-NLF wing: Experiment[27] and other predictions[28,30]

Acknowledgements

References