OPTIMAL YAW CONTROL OF A WIND FARM BASED ON COMPUTATIONAL FLUID DYNAMICS

T. Kim; J. Song; D. You

doi:10.6112/kscfe.2024.29.2.074

Preview

Original Article

Journal of Computational Fluids Engineering. 30 June 2024. 74-84
https://doi.org/10.6112/kscfe.2024.29.2.074

OPTIMAL YAW CONTROL OF A WIND FARM BASED ON COMPUTATIONAL FLUID DYNAMICS

전산유체역학 해석을 기반으로 한 풍력단지의 최적 요 제어

T. Kim¹

J. Song¹

D. You¹^†

김 태완¹

송 정환¹

유 동현¹^†

¹Department of Mechanical Engineering, Pohang University of Science and Technology

¹포항공과대학교 기계공학과

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted noncommercial use, distribution, and reproduction in anymedium, provided the original work is properly cited.

ABSTRACT

Energy production can be increased by active yaw control of wind turbines. Active yaw control can deflect the wake region of an upstream wind turbine, increasing the mean wind speed passing through a downstream wind turbine. Conventional optimization of active yaw control maximizes the power generation based on a yawed wake model. However, a yawed wake model cannot predict the blockage effect of a wind farm and the spanwise velocity in the deflected wake region. In the present study, optimal yaw control based on a yawed wake model is shown to be suboptimal in a real-world wind farm by Reynolds-averaged Navier-Stokes simulations. Considering both the streamwise and the spanwise velocity fields in a wind farm, conventional yaw control is improved to maximize the generated power.

Keywords

Computational analysis

Wind farm control

Active yaw control

Particle swarm optimization

키워드

전산해석

풍력단지 제어

능동 요 제어

떼 지능 최적화

MAIN

1. 서 론
2. 풍력단지 유동 해석
2.1 RANS 시뮬레이션
2.2 Blade element theory
2.3 Actuator disk model
2.4 후류 모델
2.5 단일 풍력발전기 수치해석
3. 풍력단지 요 각도 최적화
3.1 후류 모델을 사용한 풍력단지 발전량 계산
3.2 최적화 방법
4. 풍력단지 최적 제어
5. 결 론

1. 서 론

풍력단지의 발전량은 풍력발전기의 제어에 따라 크게 향상될 수 있다. 제어 방법에는 축 방향 유도 제어(axial induction control), 틸트 제어(tilt angle control), 능동 요 제어(active yaw control) 등이 있다. 그 중, 능동 요 제어의 경우 풍력발전기의 후류 영역을 크게 편향시키면서 풍력발전기에 가하는 구조적인 하중은 작기 때문에 가장 산업적으로 적용 가능한 기술로 연구되고 있다[1]. 따라서, 풍력단지에 특정 바람이 불었을 때 가장 높은 전력을 생산할 수 있는 각 풍력발전기의 요 각도를 찾는 연구가 많이 수행되고 있다[2,3].

이러한 능동 요 제어의 효율을 최대화하기 위해서 풍력발전기들의 요 제어에 따른 발전량을 예측하기 위한 후류 모델들이 개발되었다. Bastankhah and Porté-Agel [4]은 가우시안 분포를 기반으로 하여 풍력발전기의 회전면이 바람에 수직이 되도록 제어되었을 때의 3차원 후류 유동장을 예측하였다. 나아가, Dou et al. [5]은 풍력발전기의 회전면이 바람에 수직하지 않을 때 형성되는 3차원의 중심 대칭이 아닌 후류 유동장을 예측하였다. 이러한 후류 모델들은 후류 영역 내 주 유동 방향(streamwise direction)의 유속 결손을 성공적으로 예측하였으나 주 유동 방향에 수직인 스팬 방향(spanwise direction)의 유속 성분은 고려하지 못했다. 하지만, 풍력발전기의 요 제어로 인해 후류 영역이 편향되는 경우 편향되는 방향으로의 유속 성분은 무시될 수 없다. 예를 들어, 후류 모델을 통해 각 풍력발전기의 요 각도를 최적화하는 경우 가장 하류의 풍력발전기의 회전면은 항상 풍력단지에 불어오는 주 유동 방향에 수직이 되도록 제어되어야 한다. 본 연구에서는 유동 해석을 통해 이러한 후류 모델을 기반으로 한 요 제어 방법이 실제 풍력단지에 적용되었을 때 최대의 발전량을 얻을 수 없음을 보였다. 또한, 풍력단지에 의한 차폐 효과(blockage effect)와 요 제어에 의한 스팬 방향의 유속 성분을 고려하여 더 높은 발전량을 얻을 수 있는 요 제어 방법을 개발하였다. 이를 위해 Reynolds-averaged Navier-Stokes(RANS) 시뮬레이션을 통해 수치해석을 수행하였으며, 각 풍력발전기는 상용 풍력발전기의 전력 계수 및 추력 계수를 만족할 수 있도록 blade element theory [6]를 사용하여 모사되었다. 또한, 기존의 후류 모델을 기반으로 한 최적 요 각도를 얻기 위해서 큰 스케일의 최적화 문제에 적합한 adaptive granularity learning distributed particle swarm optimization(AGLDPSO) [7] 방법을 사용하여 최적화를 수행하였다.

2. 풍력단지 유동 해석

2.1 RANS 시뮬레이션

비압축성 유체에 대한 RANS 방정식은 다음과 같다.

(1)

\frac{\partial {\bar{u}}_{i}}{\partial x_{i}} = 0,

(2)

ρ {\bar{u}}_{j} \frac{\partial {\bar{u}}_{i}}{\partial x_{j}} = - \frac{\partial \bar{p}}{\partial x_{i}} + μ \frac{\partial^{2} {\bar{u}}_{i}}{\partial x_{j} \partial x_{j}} + \frac{\partial}{\partial x_{j}} (μ_{t} (\frac{\partial {\bar{u}}_{i}}{\partial x_{j}} + \frac{\partial {\bar{u}}_{j}}{\partial x_{i}})) + ρ g_{i} + F_{i} .

$x_{i}$ 는 위치를 나타내고, ${\bar{u}}_{i}$ 와 $\bar{p}$ 는 각각 Reynolds-averaged 속도 및 압력을 나타낸다. 𝜌, 𝜇, $g_{i}$ , $F_{i}$ 는 각각 밀도, 점도(dynamic viscosity), 중력 가속도, 유체에 가해지는 외력을 의미한다. 마지막으로 $μ_{t}$ 는 난류 점도를 의미하며, 난류 섭동에 의해 발생하는 Reynolds stress를 모사하는 데 사용된다. 전산수치해석 프로그램으로는 상용 소프트웨어인 ANSYS FLUENT(2023 R1)를 사용하였으며, 풍력단지 내 유동 해석을 위한 난류 모델은 standard $k - ϵ$ 모델을 사용했다. RANS 시뮬레이션을 통하여 풍력단지 내의 시간에 따라 변하지 않는 steady 유동을 계산하였고, 이를 바탕으로 풍력단지의 발전량을 계산하였다.

2.2 Blade element theory

풍력단지 내 유동을 해석하기 위해서는 풍력발전기로 인해 발생하는 식 (2)의 외력 항을 적절하게 모사해야 한다. 이를 위해 풍력발전기 날개의 반경 방향 $r$ 지점에서 요소 별로 가해지는 힘을 다음과 같이 blade element theory를 기반으로 계산하였다[6].

(3)

Δ F_{i} {\hat{x}}_{i} = \frac{1}{2} ρ u_{r e l}^{2} \frac{B c}{2 π r} {(C_{L} \cos ϕ + C_{D} \sin ϕ)}_{r} Δ r Δ θ,

(4)

Δ F_{i} \hat{θ_{i}} = \frac{1}{2} ρ u_{r e l}^{2} \frac{B C}{2 π r} {(C_{L} \sin ϕ - C_{D} \cos ϕ)}_{r} Δ r Δ θ .

$\hat{x_{i}}$ 는 풍력발전기의 회전면에 수직인 방향을 나타내는 단위 벡터이며, $\hat{θ_{i}}$ 는 각 날개 요소의 속도와 평행한 방향을 나타내는 단위 벡터이다. 또한, $u_{r e l}$ 은 풍력발전기 날개 요소 각각에 불어오는 바람의 상대 속도를 의미하며 𝜙는 풍력발전기의 회전면과 $u_{r e l}$ 이 이루는 각도를 의미한다. $C_{L}$ , $C_{D}$ 가 각각 날개의 양력 계수와 항력 계수를 의미하기에 식 (3)과 식 (4)는 날개에서 발생하는 양력과 항력이 $\hat{x_{i}}$ 와 $\hat{θ_{i}}$ 방향으로 투영되는 것을 의미한다. 이때 수치해석 상 실제 풍력발전기의 전력 계수 및 추력 계수를 모사하기 위해 풍력발전기 날개의 피치 각도와 회전 속도를 조정하여 날개의 양력 계수와 항력 계수에 영향을 주는 받음각(angle of attack)을 조절하였다.

2.3 Actuator disk model

풍력발전기의 회전면이 유체에 가하는 힘은 다음과 같은 actuator disk model을[8] 기반으로 적용하였다.

(5)

F_{i} = \sum_{j} Δ F_{j} \frac{1}{δ^{3} π^{3 / 2}} \exp (\frac{- r_{i j}^{2}}{δ^{2}}) .

$r_{i j}$ 는 $i$ 번째 격자와 풍력발전기의 $j$ 번째 날개 요소 사이의 거리를 나타내며, 표준편차 𝛿는 유체에 가하는 힘이 연속적으로 가해질 수 있도록 조절하는 상수를 의미한다.

2.4 후류 모델

기존의 후류 모델을 기반으로 한 최적 요 제어를 수행하기 위하여 다음과 같은 후류 모델을 사용하였다[5].

(6)

\frac{Δ u}{u_{\infty}} = (1 - \sqrt{1 - \frac{C_{T} \cos^{3} γ}{8 σ_{yaw} σ_{z}}}) \times \exp (- \frac{1}{2 σ_{yaw}^{2}} {(\frac{y - Y_{o f f s e t, z}}{D \cos γ})}^{2} - \frac{1}{2 σ_{z}^{2}} {(\frac{z - z_{hub}}{D})}^{2}) .

$u_{\infty}$ , $Δ u$ 는 각각 풍력발전기에 들어오는 바람의 속력 및 후류 영역 내부의 유속 결손(wake deficit)을 의미한다. $C_{T}$ 는 풍력발전기의 추력 계수를 의미하며, 𝛾는 풍력발전기의 요 각도를 의미한다. 이때 풍력발전기의 회전면이 들어오는 바람에 수직이 되도록 제어되는 경우 요 각도는 0°로 정의되며, + 부호는 반시계 방향의 제어를 의미한다. $σ_{z}$ , $σ_{y a w}$ 는 각각 풍력발전기 후류 영역 내부의 유속 결손의 높이 방향( $z$ ) 및 스팬 방향( $y$ ) 가우시안 분포의 형태를 나타내는 표준편차로, 풍력발전기로부터 하류 방향으로 떨어진 거리에 비례해 증가한다. 이때 풍력발전기의 중심으로부터 높이 방향 및 스팬 방향으로의 거리는 풍력발전기의 회전 직경 $D$ , $D c o s γ$ 로 각각 무차원화되어 있다. 풍력발전기의 요 각도의 절댓값이 0°를 초과하여 제어되는 경우 후류 영역은 스팬 방향으로 편향되며, 편향된 정도는 높이 방향으로 가우시안 분포를 따르는 $Y_{o f f s e t, z}$ 에 의해 결정된다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290206/images/jkscfe_2024_292_074_F1.jpg

Fig. 1.

The calculation domain of a wind turbine for a RANS simulation

Table 1.

The result of a grid convergence test

Grid cell size	Number of grid cells	Power(W)	Relative error(%)
$(0.2 D)^{3}$	56,250	2149.5	0.7688
$(0.1 D)^{3}$	450,000	2133.1	-
$(0.08 D)^{3}$	888,250	2131.5	0.0750

2.5 단일 풍력발전기 수치해석

풍력단지 내 후류 영역 및 발전량을 계산하기에 앞서 단일 풍력발전기 Vestas V112 [3]에 대해 RANS 시뮬레이션을 수행하여 격자 수렴성 분석 및 RANS 시뮬레이션과 후류 모델의 후류 유동장 차이를 분석하였다. Fig. 1은 단일 풍력발전기에 대한 계산 영역을 나타내며, 높이 방향으로는 $3 D$ 의 계산 영역을 설정하였다. 입구에는 풍력발전기의 회전 중심에서의 유속이 9 m/s가 되도록 다음 식과 같은 대기 경계층 유동을 경계조건으로 설정하였다.

(7)

u (z) = \frac{u^{*}}{κ} \log (\frac{z + z_{0}}{z_{0}}) .

해상 풍력단지를 모사하기 위하여 von Kármán 상수 𝜅는 0.4, 지면의 거칠기 높이(roughness height) $z_{0}$ 는 0.0001 m 로 설정하였다[9,10]. 풍력단지의 윗면에는 대기 경계층 유동을 만족할 수 있도록 유속 경계조건을 설정하였고, 밑면에는 no-slip 경계조건을 설정했다. 풍력단지 옆면에는 periodic 경계조건, 출구에는 출구 방향의 유속 변화가 없다고 가정하는 outflow 경계조건을 설정하여 수치해석을 수행했다.

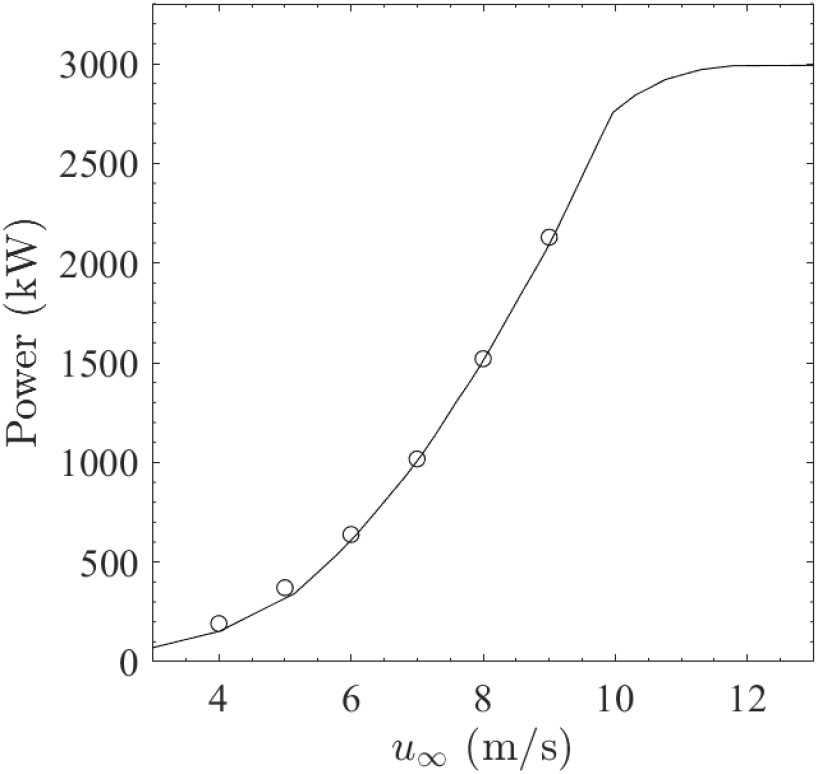
계산 영역 전체에 균일한 크기의 정육면체 격자를 생성하였으며, 격자의 한 변의 길이가 $0.2 D$ , $0.1 D$ , $0.08 D$ 일 때에 대해 Table 1과 같이 격자 수렴성 분석을 수행했다. 격자의 한 변의 길이가 $0.1 D$ 일 때와 $0.08 D$ 일 때의 풍력발전기의 발전량의 상대오차는 약 0.08%로 매우 낮게 계산되었고, 계산 비용을 고려하여 격자의 한 변의 길이를 $0.1 D$ 로 설정하여 풍력단지의 시뮬레이션을 수행하였다. 이 경우, 식 (5)의 𝛿는 시뮬레이션을 통해 계산된 발전량과 Vestas V112의 성능곡선의 차이를 최소화할 수 있도록 약 $0.143 D$ 로 설정되었다. 해당 격자를 사용했을 때 풍력발전기의 회전 중심에서의 유속이 9 m/s 이하인 유속에서 시뮬레이션을 통해 계산된 발전량은 Fig. 2와 같이 나타난다. 9 m/s의 유속을 기준으로 시뮬레이션을 통해 계산된 발전량은 Vestas V112의 성능 곡선에 따른 발전량과 약 1.7%의 작은 차이를 보였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290206/images/jkscfe_2024_292_074_F2.jpg

Fig. 2.

Power of a RANS simulation(○) is compared with that of the manufacturer’s performance curve(━)

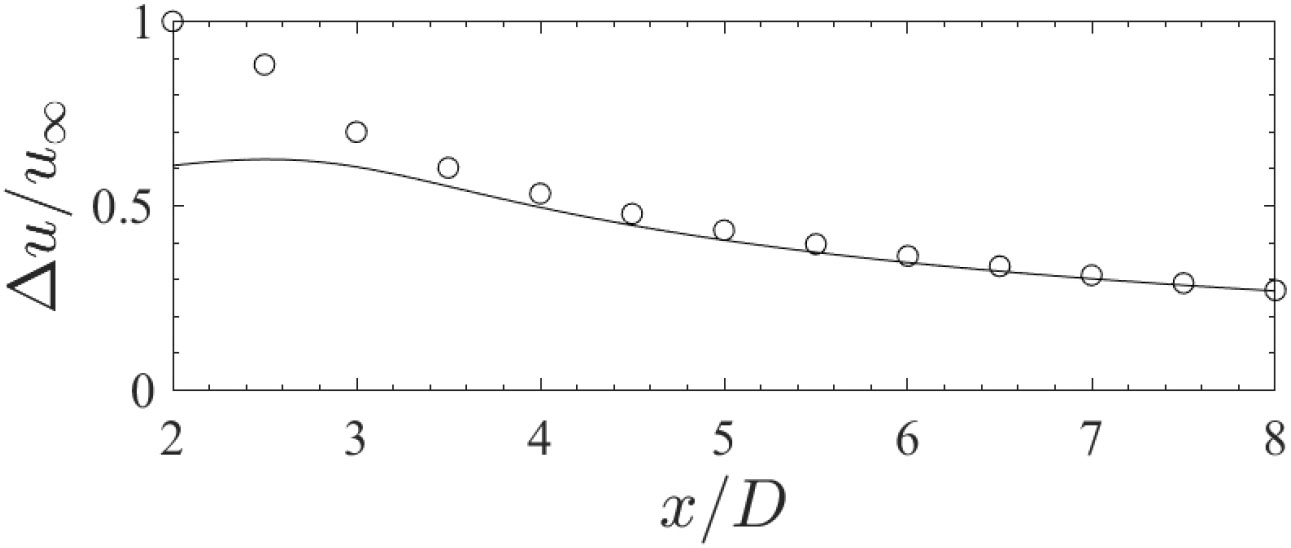
https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290206/images/jkscfe_2024_292_074_F3.jpg

Fig. 3.

The streamwise wake deficit of the wake model(○) is compared with that of a RANS simulation(━)

Fig. 3은 RANS 시뮬레이션과 후류 모델의 유속 결손을 나타낸다. 후류 모델의 경우, 풍력발전기로부터 떨어진 거리가 $3 D$ 이내인 near wake zone에서는 예측 결과가 정확하지 않으며, 특히 $2 D$ 이내의 거리는 식 (6)의 계산 결과에 허수부가 생성되어 후류 모델이 적용될 수 없다. 반면에, RANS 시뮬레이션의 유동장은 비압축성 유체에 대한 지배방정식을 기반으로 시공간적으로 충분히 수렴했기 때문에 near wake zone 내에서도 후류 모델에 비해 정확하게 유동장을 예측할 수 있다. $3 D$ 이후의 거리에 대해서는 RANS 시뮬레이션과 후류 모델의 유속 결손에 대한 평균 제곱근 오차가 약 0.0378로 계산되어 후류 모델의 유동장 예측 결과가 상대적으로 정확한 RANS 시뮬레이션의 유동장 예측 결과를 크게 벗어나지 않는 것을 확인할 수 있다.

3. 풍력단지 요 각도 최적화

3.1 후류 모델을 사용한 풍력단지 발전량 계산

각 풍력발전기의 발전량을 계산하기 위해 먼저 후류 모델을 통해 풍력단지 임의의 지점에서 주 유동 방향의 유속 $u$ 를 구한 후, 다음과 같이 $i$ 번째 풍력발전기의 회전면에 수직으로 들어가는 평균 유속 ${\bar{u}}_{i n, i}$ 를 계산한다.

(8)

{\bar{u}}_{i n, i} = \frac{1}{A_{i}} \iint_{A} u (r, θ) r d r d θ .

$A_{i}$ 는 풍력발전기 회전면의 면적을 의미한다. 바람을 먼저 맞이하는 순서대로 $i$ 번째 풍력발전기의 발전량을 다음과 같이 계산하여 상류에 위치한 풍력발전기의 후류 영역으로 인해 하류에 위치한 풍력발전기의 발전량이 감소하는 효과를 예측할 수 있도록 한다.

(9)

P = \sum_{i} \frac{1}{2} ρ C_{P} {({\bar{u}}_{i n, i})}^{3} A_{i .}

$C_{P}$ 는 풍력발전기의 전력 계수를 의미하며, 식 (9)를 통해 풍력단지 전체의 발전량 $P$ 를 계산한다.

3.2 최적화 방법

풍력단지의 발전량을 최대화할 수 있도록 요 각도를 최적화하는 문제는 다음과 같이 정의된다.

(10)

x_{o p t} = \underset{x}{argmin} C (x), x \subset ℝ^{n \times 1},

(11)

C (x) = \frac{1}{P} .

$x$ 는 $n$ 개의 풍력발전기의 요 각도를 나타내며 요 각도는 풍력발전기의 회전면이 바람에 수직한 상태가 0°로 정의되어 + 부호는 반시계 방향을 의미한다. $C (x)$ 는 최소화해야 하는 비용함수를 의미한다. 비용함수는 풍력단지의 발전량의 역수로 정의되기 때문에 최적화를 통해 찾아진 해 $x_{o p t}$ 는 풍력단지의 발전량을 최대화하는 풍력발전기들의 요 각도를 의미한다. 이처럼 정의된 최적화 문제의 전역 최적점을 찾기 위해 큰 스케일의 문제에 적합한 AGLDPSO 방법을[7] 사용하였다. 최적화를 위해 사용한 입자 $x$ 의 수는 500개이며[7], 최적화의 시작 단계에서 –90°와 90° 사이의 랜덤한 요 각도를 가지도록 초기화되었다. 이후 입자들은 최적화 단계마다 여러 개의 군집으로 분할된다. 각각의 분할된 군집 내에서 가장 비용함수 값이 큰 입자( $x_{w}$ ) 하나씩만 비용함수를 최소화하기 위해 다음과 같이 업데이트된다.

(12)

x_{w}^{t + 1} = x_{w}^{t} + v_{w}^{t},

(13)

v_{w}^{t} = ω^{t} \cdot v_{w}^{t - 1} + c_{1} r_{1}^{t} \cdot (x_{s b e s t}^{t} - x_{w}^{t}) + c_{2} r_{2}^{t} \cdot (x_{g b e s t}^{t} - x_{w}^{t}) .

위 첨자 $t$ 는 최적화 단계를 나타내며, $v_{w}$ 는 최적화 단계마다 입자가 업데이트되는 정도를 나타낸다. $ω$ , $r_{1}$ , $r_{2}$ 는 0과 1사이의 값을 가지는 랜덤 벡터이며, $c_{1}$ , $c_{2}$ 는 탐색 속도를 조절할 수 있는 변수로 각각 1.0, 0.1로 설정되었다[7]. $x_{s b e s t}$ 는 업데이트되는 입자가 포함된 군집 내에서 가장 비용함수 값이 작은 입자를 의미하며, $x_{g b e s t}$ 는 전체 입자 중에서 가장 비용함수 값이 작은 입자를 의미한다. 이러한 방법을 통하여 비용함수 값이 가장 작은 $x_{s o p t}$ 가 찾아지는데, 이때 요 각도는 –90°와 90° 사이의 값으로만 제어되도록 설정하였다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290206/images/jkscfe_2024_292_074_F4.jpg

Fig. 4.

A wind farm is shown with the black dashed line(┉), and the calculation domain of the wind farm for a RANS simulation is shown with the black solid line(━)

4. 풍력단지 최적 제어

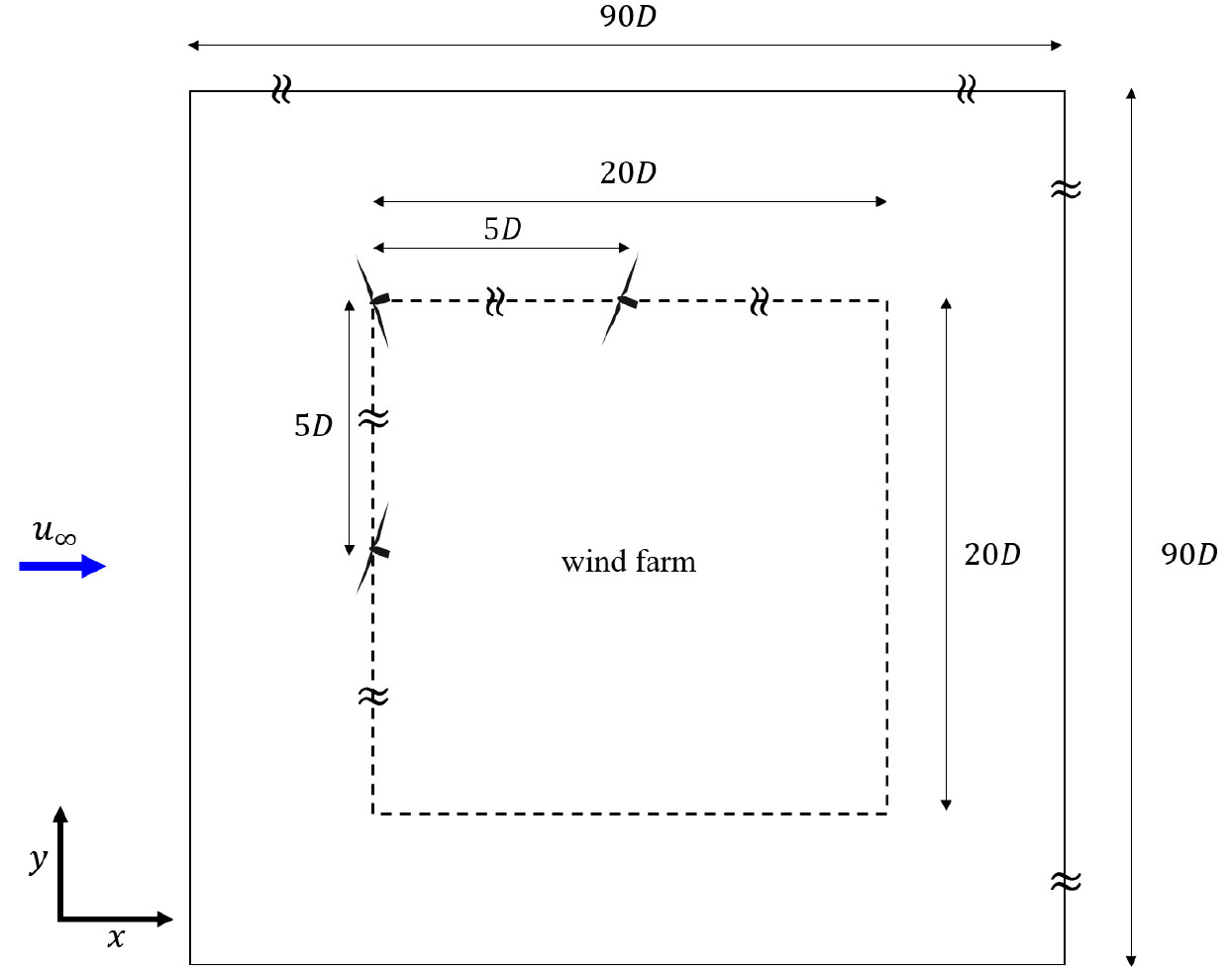
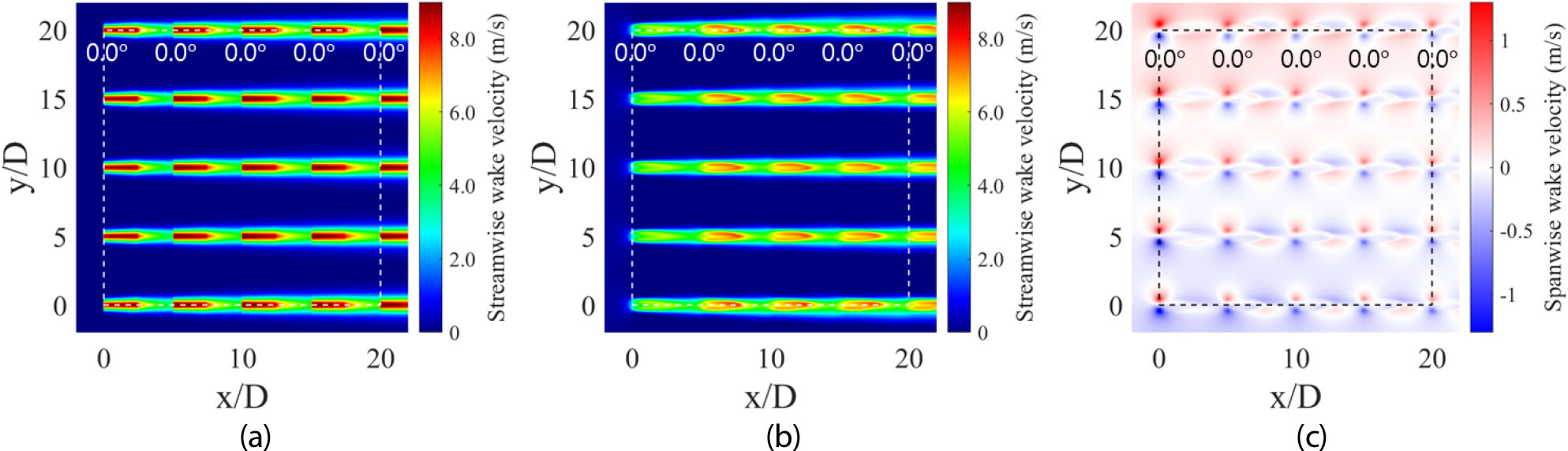
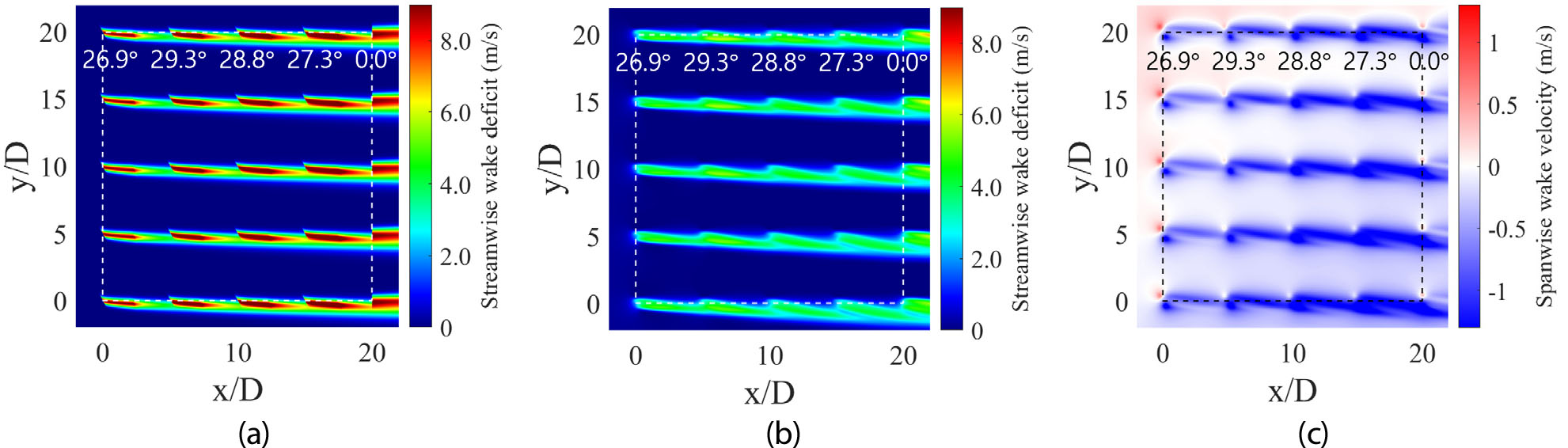
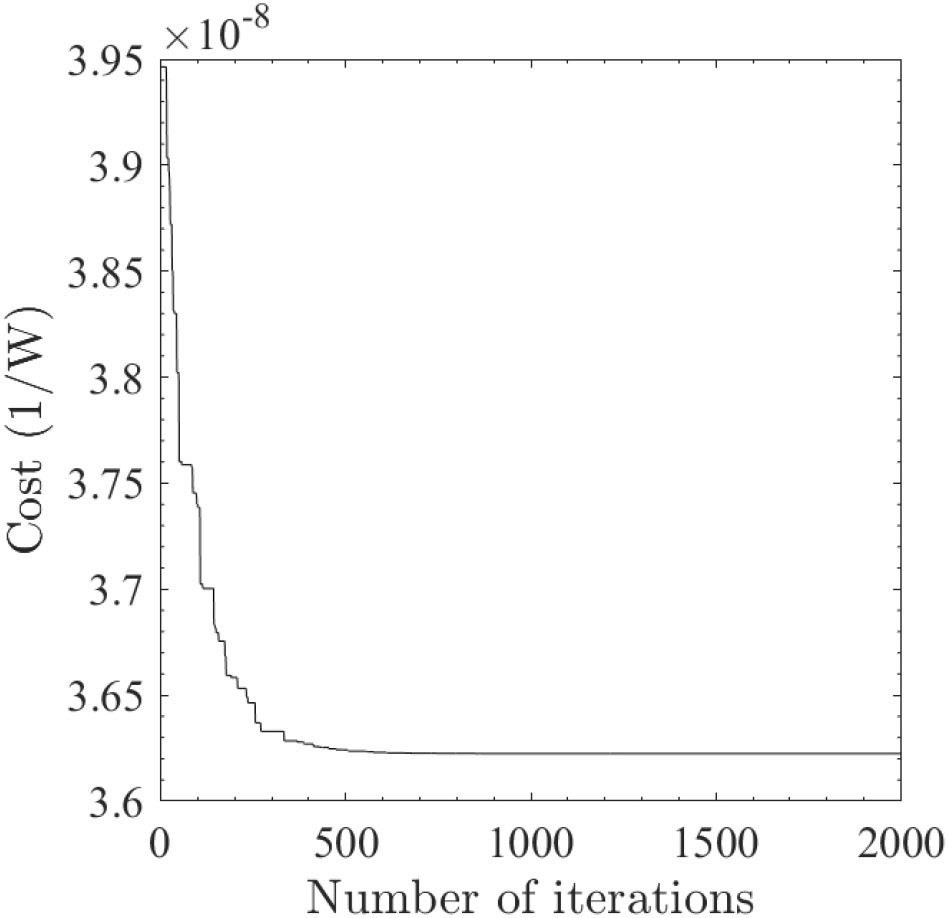
최적 제어를 수행하기 위해 Fig. 4와 같이 총 25기의 Vestas V112 풍력발전기가 각각 $5 D$ 간격의 바둑판 형태로 배치된 풍력단지를 고려하였다. 따라서, 풍력단지의 각 변의 길이는 $20 D$ 로 설정되었다. 이때 불어오는 유속 $u_{\infty}$ 는 9 m/s로 설정되었다. 이러한 풍력단지에 대해 기존의 탐욕 제어 방법은 모든 풍력발전기의 회전면들이 풍력단지에 불어오는 주 유동 방향에 수직이 되도록 제어한다. 탐욕 제어를 수행했을 때의 후류 유동장 결과는 Fig. 5에 나타나 있다. Fig. 5(a)는 후류 모델을 기반으로 한 주 유동 방향 유속 결손 결과를 나타내며, Fig. 5(b)는 RANS 시뮬레이션을 통해 계산한 주 유동 방향 유속 결손 결과를 나타낸다. Fig. 5(c)는 RANS 시뮬레이션을 통해 계산한 스팬 방향 유속 결과를 나타낸다. 탐욕 제어를 수행했을 때의 발전량은 후류 모델을 통해 19.53 MW로 계산되었으며, RANS 시뮬레이션을 수행했을 때는 20.69 MW로 계산되어 약 5.94%의 차이를 보였다. 반면에, 이러한 풍력단지에 대해 후류 모델을 기반으로 최적 제어를 수행했을 때의 후류 유동장 결과는 Fig. 6에 나타나 있다. 최적 요 제어는 후류 모델을 기반으로 발전량을 최대화할 수 있도록 최적화하여 정해졌으며, 매 최적화 단계에 따른 비용함수 값은 Fig. 7에 나타나 있다. 전역적으로 수렴한 최적화 결과를 얻기 위하여 10번의 독립적인 최적화를 수행하였으며, 최소화된 비용함수의 평균은 3.6224×10^-8 $W^{- 1}$ , 표준편차는 1.4457×10^-15 $W^{- 1}$ 로 계산되어 모든 최적화 시행을 통해 같은 최적 요 값을 얻은 것을 확인했다. 이와 같이 후류 모델을 기반으로 최적화된 능동 요 제어를 수행하는 경우의 발전량은 후류 모델을 통해 27.61 MW로 계산되었다. 따라서, 후류 모델을 통해 발전량을 계산하는 경우 능동 요 제어를 수행함으로써 탐욕 제어를 수행했을 때 대비 발전량이 약 41.4% 증가했다. 기존의 탐욕 제어 방법은 뒤쪽 풍력발전기의 발전기에 영향을 주는 후류 효과를 전혀 고려하지 않기 때문에 능동 요 제어를 수행하는 경우 상당히 높은 수준의 발전량 향상을 얻을 수 있다. 이러한 최적 제어 방법을 RANS 시뮬레이션을 통해 계산한 결과 발전량은 29.45 MW로 후류 모델을 기반으로 계산한 발전량 27.61 MW에 비해 약 6.66%의 차이가 있었다.

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290206/images/jkscfe_2024_292_074_F5.jpg

Fig. 5.

Yaw angles of wind turbines are greedy controlled based on a wake model. (a) A streamwise wake deficit contour is calculated using a wake model. (b) A streamwise wake deficit contour and (c) a spanwise wake velocity contour are calculated using a RANS simulation

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290206/images/jkscfe_2024_292_074_F6.jpg

Fig. 6.

Yaw angles of wind turbines are optimally controlled based on a wake model. (a) A streamwise wake deficit contour is calculated using a wake model. (b) A streamwise wake deficit contour and (c) a spanwise wake velocity contour are calculated using a RANS simulation

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290206/images/jkscfe_2024_292_074_F7.jpg

Fig. 7.

The cost function value as a function of the number of optimization iterations

https://cdn.apub.kr/journalsite/sites/kscfe/2024-029-02/N0500290206/images/jkscfe_2024_292_074_F8.jpg

Fig. 8.

Yaw angles of wind turbines are optimally controlled based on a RANS simulation. (a) A streamwise wake deficit contour and (b) a spanwise wake velocity contour are calculated using a RANS simulation

단일 풍력발전기와 다르게 여러 개의 풍력발전기가 모인 경우는 풍력단지의 항력에 의해 풍력단지를 돌아가는 유속이 생기는 차폐 효과(blockage effect)가 발생한다. 따라서, 풍력단지의 중심선( $y = 10 D$ )을 기준으로 $y$ 가 커질 때에는 + 방향, $y$ 가 작아질 때는 – 방향의 스팬 방향 속도 성분이 생긴다. 또한, 후류 영역 내부의 주 유동 방향 유속이 감소한 만큼 연속 방정식을 만족하기 위해 후류 영역의 바깥쪽의 주 유동 방향 유속이 증가하게 되는데, 이로 인하여 RANS 시뮬레이션을 통해 계산한 풍력단지의 발전량이 후류 모델을 통해 계산한 풍력단지의 발전량보다 높다. 따라서, 풍력단지의 차폐 효과로 인한 주 유동 방향 및 스팬 방향 유속 성분의 변화로 인하여 후류 모델을 기반으로 최적화한 요 제어 방법은 실제 풍력단지를 모사하는 RANS 시뮬레이션 상에서 최대의 발전량을 달성할 수 없다.

여기에 더하여 후류 모델은 후류 영역 내부의 스팬 방향 유속을 예측하지 못한다. 하지만, Fig. 6(c)와 같이 요 제어를 수행하는 경우 후류가 편향되는 방향인 - $y$ 방향의 스팬 방향 유속 성분이 생긴다. 풍력단지의 차폐 효과와 후류 편향으로 인해 풍력단지의 위쪽 선( $y = 20 D$ )에서 가장 먼저 바람을 맞이하는 풍력발전기의 순서대로 바람의 각도는 0°가 아닌 –2.27°, -6.52°, -8.63°, -9.42°, -7.77°로 계산된다. 이 경우, 각 풍력발전기의 요 각도를 후류 모델을 통해 계산한 최적 요 각도에서 들어오는 바람의 각도만큼 트는 경우 풍력발전기를 수직으로 지나는 평균 유속이 증가하기 때문에 더 높은 발전량을 달성할 수 있다.

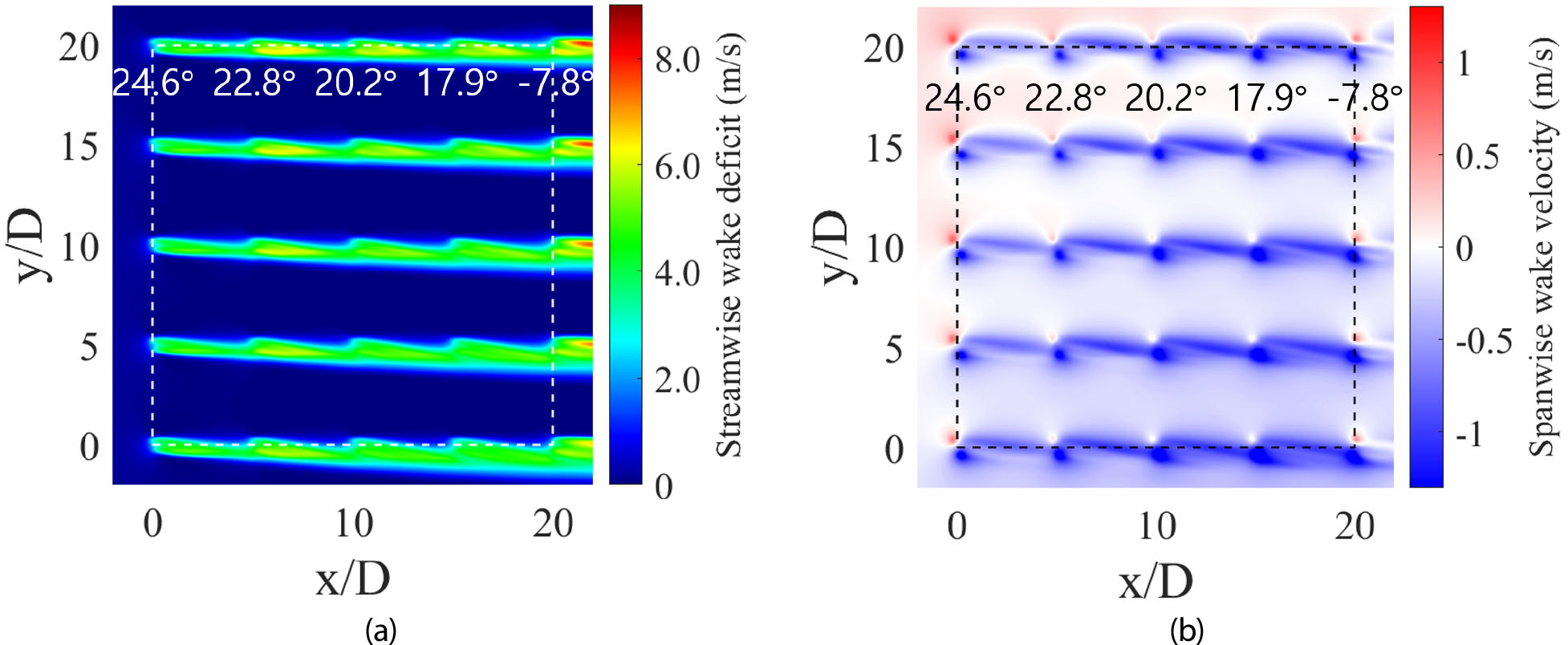
이처럼 RANS 시뮬레이션에서 계산된 스팬 방향 유동장을 반영하여 개선된 능동 요 제어를 수행한 결과는 Fig. 8과 같다. 전체 풍력단지의 발전량은 29.78 MW로 계산되어 후류 모델을 기반으로 한 풍력단지의 최적 제어에 비하여 1.12%의 추가적인 발전량의 향상을 얻었다. 특히 가장 뒤쪽의 풍력발전기의 요 각도가 0.0°가 아닌 상황에서 최대의 발전량을 얻었는데, 이러한 경향은 후류 모델을 사용하여 최적화하는 경우에는 도출할 수 없다. 또한, 풍력발전기의 요 제어로 인해 편향되는 후류의 방향을 고려하여 요 각도의 보정을 수행하기 때문에 풍력단지의 위쪽 선( $y = 10 D$ )에서 가장 먼저 바람을 맞이하는 풍력발전기의 순서대로 26.9°, 29.3°, 28.8°, 27.3°, 0.0°로 제어되었던 요 각도가 각각 24.6°, 22.8°, 20.2°, 17.9°, -7.8°로 보정되었다. 풍력발전기의 요 각도를 크게 제어하는 경우 풍력발전기에 가해지는 구조적인 하중이 증가하기 때문에[11], 이러한 결과는 본 제어 방법이 기존 방법에 비해 발전량의 향상을 보인 것과 더불어 실제 풍력단지에의 적용이 더욱 용이할 것임을 나타낸다.

5. 결 론

본 연구에서는 전산유체역학 해석을 사용하여 풍력단지의 발전량을 최대화하기 위한 요 제어를 찾는 방법이 개발되었다. 먼저, 요 제어를 고려할 수 있는 풍력발전기의 후류 모델을 기반으로 풍력단지의 요 각도를 최적화하였다. 상용 풍력발전기 25기로 이루어진 실제 스케일의 풍력단지에 대하여 후류 모델을 기반으로 요 각도를 최적화한 결과 후류 모델을 기반으로 계산한 발전량이 기존의 탐욕 제어를 수행했을 때 대비 41.4% 향상되었다. 이때, Reynolds-averaged Navier-Stokes(RANS) 시뮬레이션을 통해 발전량을 계산하는 경우는 발전량의 향상도가 42.3%로 유사한 향상도를 보이는 것을 확인했다. 즉, 후류 모델이 주 유동 방향의 유속 성분을 잘 예측하기 때문에 후류 모델을 기반으로 한 최적 요 각도를 그대로 실제 풍력단지에 적용하더라도 최적에 가까운 높은 발전량을 보장할 수 있다.

하지만, 후류 모델은 풍력단지의 차폐 효과 및 스팬 방향 유동장을 예측하지 못하는 단점이 있다. 이를 고려하여 실제 환경에서의 최적 요 제어를 통한 발전량 향상의 기대효과를 높이기 위하여 후류 모델을 기반으로 얻어진 최적의 요 각도를 보정하는 방법이 개발되었다. 구체적으로는 RANS 시뮬레이션을 통해 후류 모델을 기반으로 얻어진 최적의 요 제어를 수행한 후 실제로 각 풍력발전기의 회전면에 들어가는 바람의 각도를 계산하였다. 이후 최적의 요 각도에서 실제로 들어오는 바람의 방향만큼 요 각도를 더함으로써 풍력발전기의 회전면에 수직으로 들어가는 평균 풍속을 증가시켰다. 그 결과 RANS 시뮬레이션 상에서 추가적으로 1.12%의 발전량의 향상을 달성하였다. 본 방법을 통해 최적 요 제어를 통한 실제 풍력단지의 발전량 향상을 더욱 증대시켰을 뿐 아니라, 보정 전의 최적 요 제어 방법에 비해 요 각도 회전의 절댓값이 줄어들었기 때문에 풍력발전기에 가해지는 구조적인 하중이 감소하는 효과를 기대할 수 있다.

Acknowledgements

본 연구는 한국연구재단의 중견연구과제(NRF-2021R1A2C2092146)의 지원을 받아 수행한 연구 결과입니다.

References

2021, Zong, H. and Porté-Agel, F., "Experimental investigation and analytical modelling of active yaw control for wind farm power optimization," Renewable Energy, Vol.170, pp.1228-1244.

10.1016/j.renene.2021.02.059

2018, Song, D., Fan, X., Yang, J., Liu, A., Chen, S. and Joo, Y.H. "Power extraction efficiency optimization of horizontal-axis wind turbines through optimizing control parameters of yaw control systems using an intelligent method," Appl. Energy, Vol.224, pp.267-279.

10.1016/j.apenergy.2018.04.114

2023, Song, J., Kim, T. and You, D., "Particle swarm optimization of a wind farm layout with active control of turbine yaws," Renewable Energy, Vol.206, pp.738-747.

10.1016/j.renene.2023.02.058

2014, Bastankhah, M. and Porté-Agel, F., "A new analytical model for wind-turbine wakes," Renewable Energy, Vol.70, pp.116-123.

10.1016/j.renene.2014.01.002

2020, Dou, B., Qu, T., Lei, L. and Zeng, P., "Optimization of wind turbine yaw angles in a wind farm using a three-dimensional yawed wake model," Energy, Vol.209, p.118415.

10.1016/j.energy.2020.118415

1998, Hansen, M.O., "Basic rotor aerodynamics applied to wind turbines."

2020, Wang, Z.J., Zhan, Z.H., Kwong, S., Jin, H. and Zhang, J., "Adaptive granularity learning distributed particle swarm optimization for large-scale optimization," IEEE Trans. Cybern., Vol.51, No.3, pp.1175-1188.

10.1109/TCYB.2020.297795632224474

2011, Wu, Y.T. and Porté-Agel, F., "Large-eddy simulation of wind-turbine wakes: evaluation of turbine parametrisations," Bound.-Layer Meteorol., Vol.138, pp.345-366.

10.1007/s10546-010-9569-x

1999, Leclerc, C., Masson, C., Ammara, I. and Paraschivoiu, I., "Turbulence modeling of the flow around horizontal axis wind turbines," Wind Eng., pp.279-294.

2006, Barthelmie, R.J., Larsen, G.C., Frandsen, S.T., Folkerts, L., Rados, K., Pryor, S.C., Lange, B. and Schepers, G., "Comparison of Wake Model Simulations with Offshore Wind Turbine Wake Profiles Measured by Sodar," J. Atmos. Ocean. Technol., Vol.23, No.7, pp.888-901.

10.1175/JTECH1886.1

2018, Damiani, R., Dana, S., Annoni, J., Fleming, P., Roadman, J., van Dam, J. and Dykes, K., "Assessment of wind turbine component loads under yaw-offset conditions," Wind Energy Sci., Vol.3, No.1, pp.173-189.

10.5194/wes-3-173-2018

Journal of Computational Fluids Engineering ISSN:1598-6071(Print) 3022-6252(Online) 한국전산유체공학회지

Preview

OPTIMAL YAW CONTROL OF A WIND FARM BASED ON COMPUTATIONAL FLUID DYNAMICS

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 1.

The calculation domain of a wind turbine for a RANS simulation

Table 1.

The result of a grid convergence test

(7)

Fig. 2.

Power of a RANS simulation(○) is compared with that of the manufacturer’s performance curve(━)

Fig. 3.

The streamwise wake deficit of the wake model(○) is compared with that of a RANS simulation(━)

(8)

(9)

(10)

(11)

(12)

(13)

Fig. 4.

A wind farm is shown with the black dashed line(┉), and the calculation domain of the wind farm for a RANS simulation is shown with the black solid line(━)

Fig. 5.

Yaw angles of wind turbines are greedy controlled based on a wake model. (a) A streamwise wake deficit contour is calculated using a wake model. (b) A streamwise wake deficit contour and (c) a spanwise wake velocity contour are calculated using a RANS simulation

Fig. 6.

Yaw angles of wind turbines are optimally controlled based on a wake model. (a) A streamwise wake deficit contour is calculated using a wake model. (b) A streamwise wake deficit contour and (c) a spanwise wake velocity contour are calculated using a RANS simulation

Fig. 7.

The cost function value as a function of the number of optimization iterations

Fig. 8.

Yaw angles of wind turbines are optimally controlled based on a RANS simulation. (a) A streamwise wake deficit contour and (b) a spanwise wake velocity contour are calculated using a RANS simulation

Acknowledgements

References