1. 서 론

자연대류는 밀도차에 의한 부력에 의해 발생하는 유체 흐름으로, 대기 및 해류의 순환 등의 자연현상에서 매우 흔하게 관찰된다. 또한 실내 냉온방 시스템, 컴퓨터 회로 냉각, 원자력 발전소 냉각 설계 등의 많은 공학적 응용 분야와도 관련되어 있다. Rayleigh-Bénard(RB) 대류는 아래에서 가열되고 위쪽에서 냉각되는 조건에서 부력에 의해 구동되는 가장 대표적인 자연대류 문제이다.

Reynolds-평균 Navier-Stokes 방정식(Reynolds-averaged Navier-Stokes equation, RANS)은 많은 공학 응용 분야에서 난류 흐름을 모사하기 위해 사용된다. 자연대류 열전달 문제에서 RANS 방정식을 풀기 위해선, 난류 효과를 나타내는 Reynolds stress 및 난류 열전달을 모델해야 한다. 또한 자연대류 문제에서는 밀도차에 의한 위치에너지가 존재하며, 이 위치에너지는 부력에 의해 난류 운동에너지로 변환된다. 이 효과는 난류 운동에너지에 대한 전달방정식에서 부력에 의한 난류 운동에너지 생성항으로 나타난다. 자연대류 난류 흐름을 예측하기 위해 개발된 RANS 모델과 관련한 광범위한 내용은 Hanjalić의 리뷰 논문[1]에서 참조할 수 있다.

선행 연구들에서는 부력 효과를 반영한 RANS 모델을 개발하기 위해, 두 수직 벽이 서로 다른 온도로 가열되는 수직 자연대류 문제를 주로 고려하였다[1,2,3,4]. 수직 자연대류 문제에서는 냉각벽 근처에서는 하강하며, 가열벽 근처에는 상승하는 일정한 시간 평균 유속 장이 존재한다. 가장 단순한 난류 열전달 모델은 경사 확산 가설(Gradient diffusion hypothesis, GDH)을 가정하는 것으로, 여기서 난류 열전달은 온도 구배 와 난류 열 확산도의 곱으로 표현된다[5]. 수직 자연대류 문제는 GDH와 2-방정식 RANS 모델(k-ε, k-ω 모델 등)을 조합하여 성공적으로 예측 가능하다고 보고되어왔다[3].

반면 RB 대류 문제는 RANS 모델로 예측하기 매우 어렵다고 알려져 있다. 이 문제는 Hanjalić의 리뷰 논문[1]에서 다음과 같이 설명된다: RB 대류에서는 부력에 의해 등온 벽 근처에서 방출되는 매우 큰 규모의 열기둥과 전체 영역을 순환하는 대류 롤(convective roll)의 형태의 흐름이 존재한다. 이러한 큰 규모의 움직임은 냉각 및 가열 벽 사이의 거리와 거의 비슷한 규모의 길이 단위를 가지고 있다. 즉, RB 대류의 난류 열전달은, 이러한 큰 규모 흐름에 의해 지배되는 전역적 특성을 가진다. 반면, RANS 방정식에서 RB 대류의 시간 평균 유속은 모든 영역에서 0으로 표현된다. 일반적인 RANS 모델에서는 모델 방정식이 특정 문제의 경계조건과 초기조건과는 독립적이라고 가정하며, 이 가정은 특정 위치에서 난류의 특성이 경계조건 등에 영향받지 않는 ‘국소적’인 특성을 가질 때 성립한다. 따라서 RB 대류 문제의 ‘전역적’인 특성은, 일반적으로 사용되는 RANS 모델로는 근본적으로 다루기 어렵다.

이러한 어려움 때문에 Hanjalić의 리뷰 논문[1]에서는 모든 영역에서 평균 유속이 0임을 가정해 수직 좌표만 독립 변수로 가정된 1차원 문제로 취급할 경우, RB 대류의 장기 평균 온도 분포를 정확하게 재현할 수 있는 모델은 없다고 언급하고 있다. 구체적으로, RB 대류의 난류 열전달은 GDH로 예측하기 매우 어려우며, 이는 높은 Rayleigh(Ra) 수 조건에서 열 경계층을 제외한 영역 대부분에서 온도 구배가 0에 가깝기 때문이다. 이에 대한 대안으로 Hanjalić & Vasić[6]은 난류 열전달의 예산방정식에 약한 평형 가설을 도입하는 방식으로 부력 효과를 포함한 대수적 난류 열전달 모델(algebraic heat flux model, AHFM)을 제안하였다. AHFM은 온도 구배 뿐만 아니라, 온도 섭동의 분산과 중력의 상호작용을 추가로 고려하기 때문에, 중심부 온도 구배가 작고 난류 열전달은 큰 문제들을 다루기 효과적이다. 그러나 정확한 RANS 시뮬레이션 결과를 얻기 위해선 난류 열전달뿐만 아니라, 난류 운동에너지(k) 및 난류 운동에너지에 대한 소산율(ε) 등에 대한 전달방정식을 정확히 모델 해야 한다. 현재 공학 응용 분야에서 많이 사용되는 2-방정식 모델에서 부력 효과를 정확히 다루는 방법은 알려지지 않았으며, 예를 들어 k-ε 모델의 ε-방정식의 부력 효과를 적절하게 모델 할 수 있는 합의된 방법은 현재까지 도출된 바 없다[7].

우회적인 대안으로, Kenjereš & Hanjalić[8,9,10,11]은 RANS 방정식에서 시간 미분항을 포함 시키고, 시간에 따라 변화하는 유동장을 계산하는 비정상 RANS(unsteady RANS, URANS) 방법을 사용하면 2차원 혹은 3차원 RB 대류를 성공적으로 예측할 수 있다고 주장하였다. Kenjereš & Hanjalić[8]은 표준 k-ε 모델에 AHFM을 결합한 모델로 URANS 시뮬레이션을 처음 수행하였고, 이후 후속 연구들[9,10,11]에서도 약간의 모델 수정과 함께 유사한 방법으로 URANS를 수행하여 Rayleigh 수 10⁵-10¹⁵ 범위에서 정확한 Nusselt 수를 재현하였다. 이는 GDH와 표준 k-ε 모델을 사용한 URANS는 Rayleigh 수 10⁸에서 실험에 비해 Nusselt 수를 약 50% 과소 예측하는 것[8]과 비교해 훨씬 정확한 결과라고 언급되었다. 수행된 URANS의 정확한 예측 결과는, 문제 영역 전체를 순환하는 대류 롤을 성공적으로 재현할 수 있기 때문이며 이를 통해 정확한 열 경계층을 모사할 수 있기 때문이라고 설명되었다. 선행연구들에서는 URANS를 수행하기 위한 계산 비용이 큰 와류 모사(large-eddy simulation, LES)와 비교하여 훨씬 적으며, 이는 공학적 응용 분야에서 URANS의 실용성을 보여준다고 주장하였다. 다른 저자를 통해 수행된 연구 중에서는, Choi[12]에 의해 k-ε 모델, AHFM, 및 elliptic relaxation 모델이 결합 된 2차원 RB 대류에 대한 URANS 시뮬레이션이 수행되었으며 앞선 연구들과 거의 같은 결과를 보고하였다. 현재까지 저자의 조사로는, RB 대류에 관련된 RANS 시뮬레이션 연구는 여기서 언급된 논문들로만 국한된다.

학술적인 관점에서는, URANS는 본질적으로 엄밀한 예측의 도구로 사용되기 힘들다고 여겨지며, 난류 모델에서 일반적으로 가정되는 국소성을 보장하기 위해선 LES와 같은 다른 난류 모델링 방법을 사용할 필요가 있다고 여겨진다[13]. 그러나 아직까지도 많은 공학 응용 분야들에서는 LES에 필요한 충분한 컴퓨터 계산 용량을 감당할 수 없어, 그 대안으로 RANS 혹은 URANS 시뮬레이션 방법이 주로 활용되고 있는 것 또한 현실이다. 이 맥락에서, URANS 방법이 자연대류 난류 흐름을 예측하는 데 과연 어느 정도 신뢰할 수 있는가에 대한 문제는, 정성적인 방법을 사용해서라도 한 번쯤 검토되어야 할 필요성이 있다고 판단된다.

기존 선행연구들에서 URANS는 주로 터보 기계, 교반 탱크, 블러프 바디 뒤 등과 같은 문제들에서 주기적으로 변하는 흐름을 효율적으로 예측하기 위해 사용되어왔다[14]. 이러한 문제들을 URANS로 예측하는 방법론의 정당성에 관해, Wilcox[13]는 난류 모델에서 예측하는 유속 섭동의 크기가 URANS에서 직접 포착하는 유속 크기보다 약 10퍼센트 이하로 작을 때, RANS 모델링에 사용된 평형 가설들이 URANS에서도 유효할 것으로 추정하였다. 하지만, 이런 정의는 수학적으로 엄밀할 수 없다는 한계를 인정하며 더 엄밀한 접근 방식을 사용하려면 LES와 같은 대체 방법이 필요하다고 설명하였다[13]. 다른 관점으로, Durbin[14] 및 Laccarino et al.[15]는 vortex shedding 문제에서 발생하는 주기적 흐름에서, 난류 에너지에 대한 주파수 스펙트럼을 보면 shedding frequency에서 다른 주파수 영역과 구분되는 날카로운 최고점(sharp peak)이 관측되며, 이러한 최고점은 일관되고 주기적인 소용돌이 흘림 구조에 의해 발생하므로 URANS에서는 이를 모델링하는 대신 이 속도장의 시간변화를 직접 반영하는 방식을 채택하는 것이 더 적절하다고 설명하였다.

반면 RB 대류를 재현하는 데 사용된 URANS가 어떻게 정확한 Nusselt 수를 예측할 수 있었는지에 대한 검토는, 앞선 예시들과는 다른 관점의 분석이 필요하다. 예를 들어, RB 난류 대류의 난류 에너지에 대한 주파수 스펙트럼에서는 앞선 와류-흘림 문제와 같이 다른 주파수 영역과 구분되는 날카로운 최고점이 관측되지 않는다는 차이점이 있다[16]. 또한 자연대류 난류 흐름에서는 열 경계층과 대류 롤이 상호작용하며 방출되는 열 기둥(thermal plume)이 열전달을 결정짓는 중요한 특징임에도 불구하고[17], LES보다 훨씬 큰 격자를 사용하는 URANS 방법에서는 이를 정확하게 재현할 수 없다는 근본적인 한계가 있다. 또한 유속, 진동 주파수와 같은 대류 롤의 구체적인 특성을 URANS가 정확히 예측할 수 있는지 여부도 불명확하며, 또한 대류 롤의 재현이 난류 열전달을 예측하는 데 어느 정도의 영향을 미치는지도 불명확하다.

임의의 문제에서, URANS가 어떤 결과를 왜 그렇게 도출하는지를 정확히 분석하기란 매우 어렵다. 이는 RANS 모델이 다수의 전달방정식 모델, 대수적 모델, 벽 근처의 감쇠 함수 등이 비선형적으로 서로 얽혀 매우 복잡하게 구성되어 있는 시스템이기 때문이다. 이 중, AHFM과 같은 대수적 모델들의 경우는 직접 수치 모사(direct numerical simulation, DNS) 방식으로 난류 통계 데이터를 수집하고, 모델 식에 수집된 데이터를 직접 대입해 그 모델의 성능을 비교하는 a priori 테스트로 검증할 수 있다[4]. 그러나 k-ε 모델의 ε-방정식과 같은 전달방정식 형태로 제시된 모델의 경우, a priori 테스트로 그 모델의 정당성을 검토할 수는 없다. 대신, 전달방정식을 포함한 RANS 모델 시스템 전체를 정당화하기 위해선 선언된 모델이 어떤 문제에서 어떤 해를 예측하는지를 경험적으로 검토해야 한다. 예를 들어, k-ε 및 k-ω RANS 모델과 같은 2-방정식 모델의 경우, 균질 전단 흐름, 균질 감쇠 난류 흐름, 채널 흐름의 log-law 영역의 상사해(similarity solution)를 재현할 수 있는 모델의 정확한 이론 해가 알려져 있으며, 이 이론해를 기준으로 모델 계수들을 최적화하는 방식이 가장 보편적으로 사용된다[5,13,14]. 그러나 자연대류 난류 문제들에 관련해선, 모델의 기준이 되는 정확한 분석 해가 존재하지 않으며, 특히 ε-방정식에 포함된 부력항의 모델 방법 및 모델 상수의 일반적인 결정 방법에 대해선 현재까지도 명확하게 확립된 기준이 존재하지 않는다[7].

본 연구의 목표는, RB 대류 문제에서 URANS가 어떤 해를 예측하는지를 정성적으로 추정하는 것이다. 다만 본 연구에서 분석할 대상은 영역 전체를 순환하는 대류 롤이 존재하며 난류 운동에너지, 소산률, 난류 열전달 등이 공간과 시간에 따라 변할 수 있는 매우 복잡한 문제를 다룬다. 이 분석을 위해, 극도로 단순화된 어림 추정법이지만, 본 연구에서는 URANS에서 모델이 예측하는 난류 점성도 및 난류 열 확산도를 전체 영역에서 단일한 값으로 대표된다고 근사하여 논의를 진행하고자 한다. 이 방법은 당연히 엄밀할 수 없는 어디까지나 ‘정성적인 추정’이지만, 현실적으로 URANS의 모든 복잡성을 고려하여 모델이 도출하는 해의 결과를 이해하는 것은 매우 어렵기 때문에 택한 우회적인 대안이다. 본 논문의 분석을 통해, URANS 모사가 주어진 Rayleigh 및 Prandtl 수 조건에서 모델링된 난류 변수들과 난류 열전달을 어떻게 예측할 것인가에 대한 경향성은 다소 설명될 수 있을 것이라 기대한다.

2. 비정상 레이놀즈-평균 시뮬레이션에서 관측되는 유동 특성

2.1 RB 대류의 유동 특성

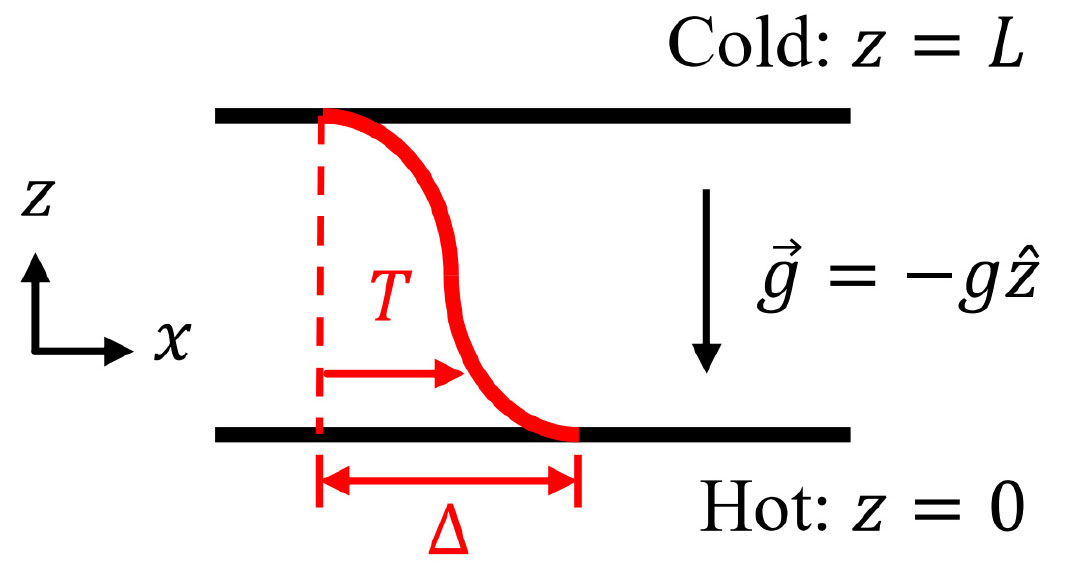
Fig. 1은 RB 대류의 문제 조건 및 온도 분포를 나타낸다. 중력이 아래 방향 g→=-gz^로 작용하는 상황에서, 서로 거리 L만큼 떨어진 두 수평 평판은 등온 경계조건을 가진다. 차가운 위쪽 벽과 따뜻한 아래쪽 벽의 온도차는 Δ이며, 유체의 밀도 𝜌는 Boussinesq 근사에 의해 ρ=ρ0β(T-T0) 식으로 변화함을 가정한다. 여기서 T는 온도, β는 열팽창률이다.

Fig. 1.

Configuration of the Rayleigh-Bénard convection analyzed in this study

운동량 및 열 수송 방정식을 무차원 화 하면, 이 문제에 대한 무차원 입력 변수는 Rayleigh(Ra) 수와 Prandtl(Pr) 수, 난류 열전달을 나타내는 무차원 출력 변수는 Nusselt(Nu) 수로 정리된다:

여기서 α는 열 확산도, uz는 z-방향 유속, <·>A는 수평 평판과 평행한 가상의 면에서의 공간 및 시간에 대한 평균을 나타낸다. RB 대류 문제의 수동력학적 안정성을 계산하면, 등온 벽이 모두 미끄럼 방지(no-slip) 조건일 때 임계 Rayleigh 수 Rac=1708가 계산된다[18]. Ra<Rac일 경우, 유동장에 대한 작은 섭동(perturbation)은 시간에 따라 감쇠되어 사라지게 된다. 따라서 이 경우에는 대류에 의한 열전달이 0이며, 식 (1)에서 Nu=1이 된다.

Fig. 2.

Schematic of convection rolls in Rayleigh-Bénard convection problems

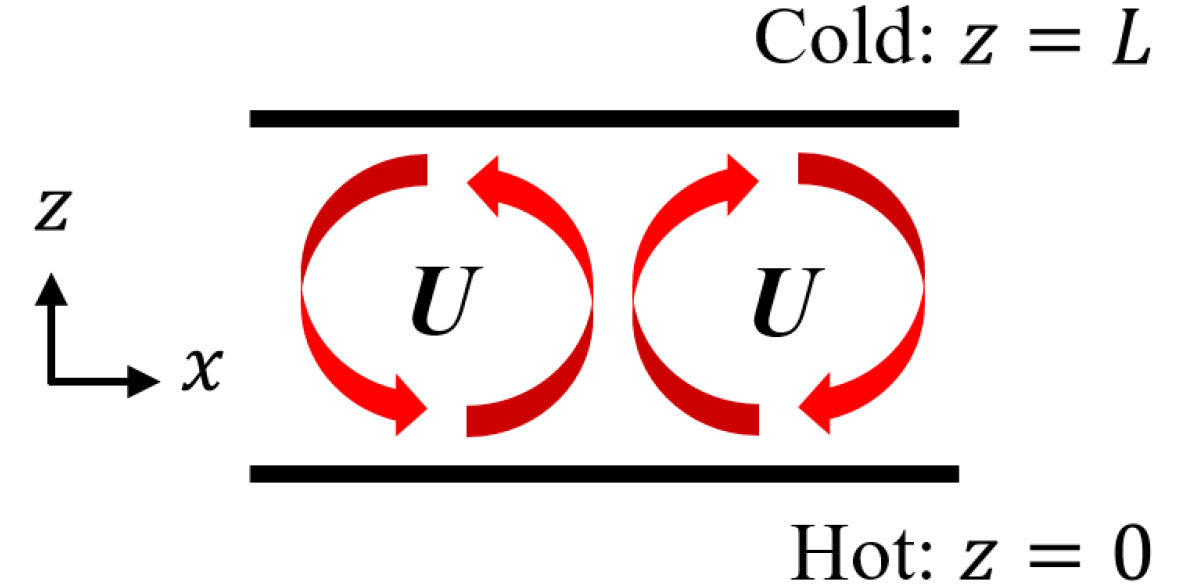
만약 Ra가 Rac보다 아주 약간 큰 값을 가질 경우, Fig. 2와 같이 두 수평 평판 사이를 2차원으로 회전하는 안정된 층류 흐름이 관측될 수 있다. 매우 넓은 수평 평판에서 0.7≤Pr≤10⁴의 유체를 사용하여 수행된 Krishnamurti의 실험 연구[19]에서는, Rac<Ra<13Rac의 좁은 범위에서 2차원 층류 대류 형태의 안정된 움직임이 관측되었다. 13Rac보다 더 큰 Ra에서는 한쪽으로 회전하는 2차원 대류에서, 중력 방향을 수직축으로 한 다른 모드의 회전효과가 추가되는 bimodal 대류가 관측되기 시작한다. 만약 Ra가 더 커질 경우, 대류 롤의 움직임은 매우 불규칙해지기 시작하며 보통 이를 난류 유동으로 분류한다[20]. 넓은 수평 평판의 경우[19] 난류로 천이되는 기준 Rayleigh 수를 Rat라고 할 때, 1≤Pr≤10범위에서 Rat=3Rac~20Rac의 값으로 관측되며, 이때 Rat의 값은 Pr이 커질수록 같이 커진다. 만약 Pr이 0에 가까워 지면 난류로의 천이는 임계 Rayleigh 수와 거의 같은 Rat≈Rac에서 일어난다. 천이 레일리 수 Rat는 문제의 기하학적 형태와 종횡비에도 영향받는다. Ahlers & Behringer[21]은 실린더에서 종횡비 𝛤(=실린더 반지름 / 높이)에 따라 달라지는 Rat를 측정하였다. 고정된 Pr=0.8에서 종횡비에 따른 측정된 Rat 값은 다음과 같다: 𝛤=57에서 Rat≈Rac; 𝛤=4.72에서 Rat=2Rac; 𝛤=2.08에서 Rat=11Rac. 레일리 수가 10⁷이상에서는 층류 대류 롤에서 관측되는 육각형 패턴과 같은 구별은 거의 사라지며[20] 이때 열 경계층의 두께는 수평 평판 사이 길이 L보다 훨씬 얇아지며, 열 경계층이 수직한 방향으로 떨어져 나가는 판 모양-열기둥의 형태의 흐름이 관측된다[17].

난류 RB 대류에서, 대류 롤 및 큰 스케일의 열 기둥의 움직임은 그 유속과 반전 주파수로 특징지어진다[17]. 대류 롤이 발생하는 이유와 그 특성을 이론적으로 이해하기 위한 선행연구 중 하나로써, Araujo et al.[22]는 대류 롤을 횡방향 무게중심, 종방향 무게중심, 회전 각속도라는 3개의 매개변수를 가진 문제로 단순화하여 열 경계층에서 분리된 단일 열 기둥의 힘과 열 균형에 대한 이론적 근사식으로 산출하였다. 산출된 이론적 근사식은 Lorenz system과 매우 유사한 형태를 가지고 있으며, Rayleigh 및 Prandtl 수의 범위에 따라 대류 롤의 움직임이 “균일한 순환(Uniform circulation)”, “혼돈스러운 반전 (Chaotic reversals)”, “주기적 반전(Periodic reversals)” 중 하나의 경향성으로 나타나는 것을 설명할 수 있었다. 또한 산출된 이론적 근사식을 이용하여 제곱근 평균 속도로 정의된 Reynolds 수와 반전 주기에 대한 무차원수를 Rayleigh 및 Prandtl 수에 대한 멱법칙으로 제시하였다.

난류 열전달을 나타내는 Nusselt 수에 대해선 층류 대류가 난류 대류로 전환될 때의 불연속성은 존재하지 않는다. 즉 고정된 Pr에서, Nu는 Ra>Rac 범위에서 Ra가 증가함에 따라 연속적으로 단조 증가한다. 난류 영역에서는 더 이상 분석적 방법으로 대류 롤의 패턴과 그 열전달의 특성을 예측하기가 매우 어려워진다. 따라서 이런 난류 흐름의 특성을 이해하기 위해선 현상학적 가설로부터 정성적인 Nu~RaaPrb의 멱법칙 관계를 추정하는 방법이 사용된다. 난류 RB 대류를 설명하기 위한 이론적 연구로써, Grossmann & Lohse[23]은 대류 롤의 형태로 나타나는 대규모 일관된 흐름(large-scale coherent flow, LSC)의 존재를 가정하고, 난류 운동 에너지와 온도 분산에 대한 소산율(dissipation)을 각각 경계층 흐름 영역과 나머지 영역으로 구분해 개별적으로 추정하는 방법을 제안하였다. 이후 Pr≈1 및 10¹²이하의 Rayleigh 수 조건에서는, LSC가 등온으로 가열되는 벽을 근처를 지나가는 유속이 느려서, LSC가 유발하는 경계층의 특성이 층류에 가깝다고 지적하였다. 이 추정으로부터 RB 대류의 운동량 및 열 경계층 두께를 LSC의 유속과 길이를 대입한 Prandtl-Blasius 경계층 이론으로 계산하였다. 이 방식으로, Nusselt 수를 Rayleigh 및 Prandtl 수에 대한 이론적 멱법칙으로 산출할 수 있었으며, 이는 대류 롤이 자연대류 난류 열전달을 주요하게 결정하는 한 가지 요소임을 추정하게 해 준다.

2.2 선행 URANS 연구에서 관측된 자연대류 유동 특성

Kenjereš & Hanjalić[8,9,10,11]의 선행 연구에서 수행된 RB대류에 대한 URANS 모사에서는, 높은 Ra범위에서 모델이 예측하는 유동 장이 난류 유동과 매우 유사한 불규칙한 대류 롤의 형태로 관측된다. Ra≥10⁹의 URANS 시뮬레이션으로 얻어진 순간 속도장 결과[11]에서는 경계층에서 떨어져나온 열기둥이 매우 복잡하게 얽혀 있는 전형적인 난류 흐름의 모습을 보인다.

URANS 모사에서는 온도 및 속도장이 시간에 따라 변하기 때문에, URANS의 대류 롤의 움직임이 직접 포착되는 효과 또한 열전달에 영향을 미친다. 구체적으로, RANS 모델에서 온도에 대한 레이놀즈 평균 전달방정식은 다음 식과 같다:

여기서 T 및 τθi는 온도와 모델링 된 난류 열전달을 나타낸다. URANS 상황에서는 T와 τθi는 공간과 시간에 따라 변하기 때문에, 통계적으로 수렴된 전체 열전달 값은 “모델링된 열전달 효과”와 “해석된(resolved) 난류 열전달 효과”로 나눌 수 있다. 이 모든 열전달 효과를 고려하여 하나의 식으로 기술하면 다음과 같다:

여기서 Uz는 URANS에서의 z-방향 유속이다. 는 해석된 열전달, 는 모델링된 난류 열전달, 는 분자 열 확산도에 의한 열전달을 나타낸다. 모든 높이에서 시간평균 총 열전달량은 Qtotal은 일정하다.

선행 URANS 연구에서는 식 (3)에서 정리된 각각의 열전달 기여도를 높이에 따른 그래프로 비교하였으며, 여기서 관측된 결과를 개략도로 다시 그린 결과를 Fig. 3에서 확인할 수 있다. RB 대류의 높은 Ra에서는 열 경계층 두께 δθ는 전체 도메인 길이 L에 비해 매우 얇다. 열 경계층 흐름 영역에서 난류 열전달의 값은 0에 가까우며, 온도는 각 등온 벽 사이의 평균 온도 값으로 매우 빠르게 변화한다. 열 경계층에서의 열전달 균형식 Qtotal=αΔ/δθ으로 부터, 열 경계층의 두께는 δθ/L~Nu-1의 값으로 추정됨을 알 수 있다. 이 때문의 Fig. 3의 Solid line으로 표현된 전체 난류 열전달량은 벽에서 0의 값을 가지며 열 경계층 영역 내에서 매우 빠르게 상승한 뒤, 경계층 바깥 영역에서 거의 균일한 값을 가지게 된다.

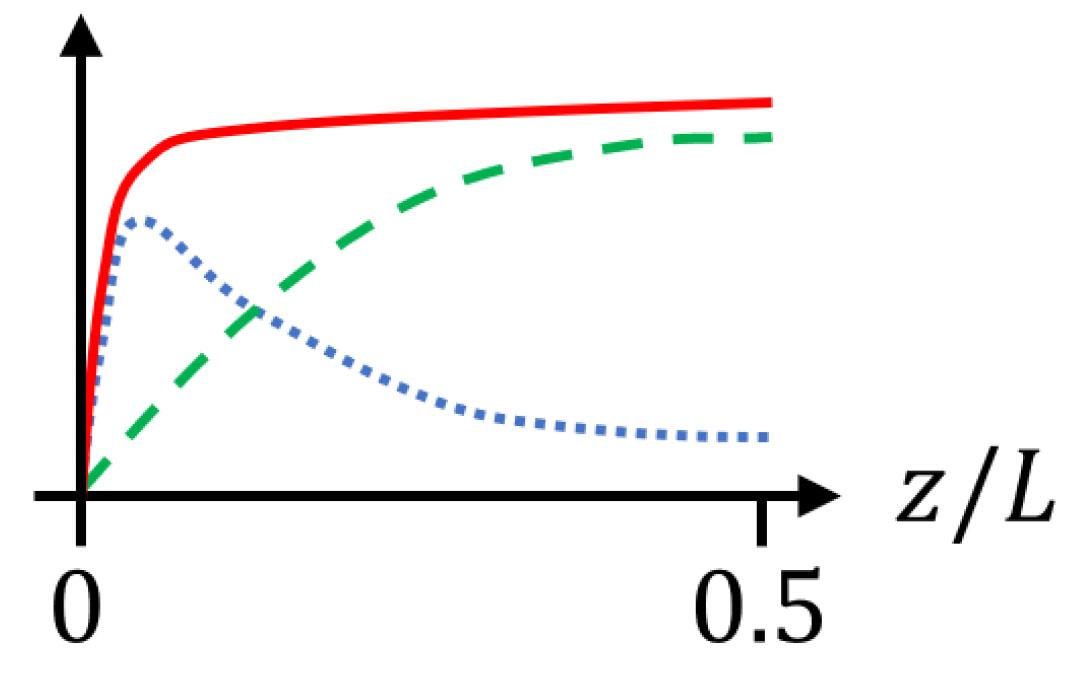
Fig. 3.

Schematic depiction of turbulent heat transfer at Ra=10⁷, as described in prior URANS research on RB convection [8,11]. Each line represents a component of heat flux: solid red line for total heat flux ; green dashed line for the resolved portion of turbulent heat flux ; and blue dotted line for modeled turbulent heat flux

선행 URANS 시뮬레이션 결과에서 가장 특징적인 점은, Fig. 3에서 볼 수 있듯이 모델로 예측된 난류 열전달 값에 비해 직접 해석된 난류 열전달 값 의 기여도가 전혀 작지 않다는 점이다. 또한 문제 조건의 Ra가 커질수록 의 상대적인 기여도는 더욱 커지며, 모델 난류 열전달은 점점 더 작아지는 경향성이 관찰되었다[11]. 이러한 선행 연구 결과를 정성적으로 이해해 보기 위해, 왜 URANS 시뮬레이션 결과에서 Ra가 커질수록 모델링된 난류 열전달의 효과가 더 작아지는지에 대한 경향성을 모델 방정식 그 자체로부터 추론해 보고자 한다.

3. 정성적 분석을 위한 단순화 방법 제안

Kenjereš & Hanjalić[8,9,10,11]의 선행연구에서는, 수행된 RB대류에 대한 URANS가 성공적으로 난류 열전달을 예측할 수 있었던 이유를 대류 롤을 성공적으로 캡쳐 할 수 있었기 때문이라고 설명되었다. 이 경향성은 Fig. 3에서 확인할 수 있으며, 대류 롤의 효과를 나타내는 직접 해석된 난류 열전달 값 의 기여도는 영역 중심부에서 전체 열전달량과 거의 같을 정도의 매우 큰 값을 가진다.

하지만 URANS 모사에서 구체적으로 대류 롤이 난류 열전달 예측에 어떤 이바지를 하는지 불분명하며, 대류 롤로 인해 전달되는 열 유속 이 왜 Ra가 커질수록 더 중요해지는지 설명되지 않았다. RANS 모델에서 도출되는 결과를 직관적으로 이해하기 어려운 이유는, RANS 모델은 k 및 ε과 같은 다수의 전달방정식 모델, 대수적 모델, 및 댐핑 함수들이 서로 내재적(implicit)이고 비선형적인 방식으로 결합하여 구성된 매우 복잡한 시스템이기 때문이다.

난류는 유체 흐름에서 온도 및 운동량 등을 매우 크게 확산시키는 효과가 있다. 이 효과를 모델링하기 위해 사용되는 가장 단순한 방법은 레이놀즈 응력 및 난류 열전달에 대해 단순 난류 점성/열 확산도 모델(simple turbulent viscosity/diffusivity model)을 사용하는 것이다. 이 상황에서 운동량과 온도의 전달방정식은, 단순히 유효(effective) 점성 νe=νt+ν, 유효 열 확산도가 αe=αt+α로 증가한 일반적인 전달방정식과 같아진다. 여기서 νt와 αt는 공간에 따라 다른 값으로 분포하며, URANS의 경우 시간에 따라서도 변할 수 있는 값이다.

극도로 단순화된 방법이지만, 우선 난류 모델이 전 공간 영역에서 시간 및 공간적으로 균일한 난류 점성도 νt와 난류 확산도 αt를 예측한다고 가정해보자. 이제 모델 Rayleigh 수, 모델 Prandtl 수, 모델 Nusselt 수를 다음과 같이 정의해 보고자 한다:

이제 회전속도 U 지름 L의 대류 롤이 URANS의 난류 열전달 예측에 미치는 영향을 추정해 보고자 한다. URANS 상황에서는 전체를 회전하는 대류 롤이 존재하며, 모델이 아닌 대류에 의해 수송되는 열이 확인되었다. 이 상황은 식 (3)의 관계식과 유사하게 다음과 같이 이해할 수 있다:

여기서 (αe/α)는 모델로 인해 증가한 난류 열 확산도를 반영한다(Fig. 3의 ). 반면 Num은 1보다 크며, URANS에서 직접 포착하는(resolved) 대류 롤의 영향을 나타낸다(Fig. 3의 ).

2.1절에서는 실제 RB 대류에서 난류로의 천이가 일어나는 Rat에 대해 설명하였다. Rat는 문제의 기하학적 조건과 Prandtl 수에 따라서 달라지지만 대략적으로 Rat≲O(105)의 값에서 난류로의 천이가 이루어진다. 균일한 난류 점성도 νt와 난류 확산도 αt를 가정한 가상적인 상황에서도, Ram>Rat일 때 URANS 시뮬레이션에서 유동장의 특성 또한 난류의 특성을 보일 것이다.

이 설명은, 2.2절에서 언급된 선행 URANS 시뮬레이션 결과에서 유동장의 특성이 난류와 매우 가까운 불규칙한 모습을 보인다는 선행 연구의 보고와 일관된다. 만약 URANS의 유동장이 난류의 특성을 가질 경우 Num은 1보다 유효하게 큰 값을 가지게 된다.

4. 모델에서 예측되는 대류 롤의 발생

정상상태 RANS 모사로 RB 대류 문제를 풀 경우, 시간 평균 유속은 모든 영역에서 0이다. 반면 URANS로 RB 대류 문제를 풀 때는 유속 U, 지름 L으로 특징지어지는 불규칙한 대류 롤이 관측된다. 선행 URANS 논문들[1,8,9,10,11]에서는 RB대류 문제에서 활용되는 URANS 방법론이 유효한 이유는, 난류 섭동의 시간 스케일과 대류 롤의 움직임이 구분되기 때문이라고 주장되었다. 더 나아가 URANS에서 성공적으로 대류 롤을 재현할 수 있기 때문에, 난류 열전달을 정확하게 예측할 수 있다고 주장하였다.

위 주장을 검토해 보기 전에, 우선 RB 대류에서 실험적으로 관측되는 대류 롤의 특성을 간략히 언급하고자 한다. 최근 매우 높은 Ra에서 수행된 2차원 직접 수치 모사[24]에서는, Ra≤10¹³ 범위에서 영역 전체를 회전하는 대류 롤이 존재함이 보고되었다. 넓은 Ra 범위에서 관측되는 대류 롤들의 회전에 대한 지름은 수평 평판 사이 거리인 L로 거의 유사하지만, 대류 롤의 속도 U 및 회전 반전의 주파수 ω는 Ra에 따라 달라진다. 구체적으로, 10⁷≤Ra≤10¹⁰ 및 Pr≈5.5범위에서, 회전속도에 대한 Reynolds(Re) 수는 대략 Reu=UL/ν~Ra0.46에 비례하며, 회전 반전의 주파수 또한 Reω=L2ω/πν~Ra0.46의 관계가 보고되었다. Araujo et al.[22]는 이 큰 규모 대류 롤의 움직임을 열 경계층에서 분리된 단일 기둥의 힘과 열 균형에 대한 이론적 근사식으로 산출하였고, 이론에서 예측한 대류 롤의 스케일 특성은 10^-2≤Pr≤10³, 10⁷≤Ra≤10¹² 범위에서 Reu~Ra0.44+-0.03Pr-0.71+-0.05 및 Reω~Ra0.44Pr-0.64으로 계산되었다.

우선, 3절에서 도입했던 난류 점성도 νt와 난류 확산도 αt가 공간 및 시간에 대해 균일한 가상적 상황을 상정해 보자. 이 상황에서의 URANS는 이 자연대류의 특성은 동점성이 νe=νt+ν, 열확산도가 αe=αt+α에 대한 실제 자연대류 유동과 똑같은 결과를 주어야 한다. Ram>Rat이기만 하면, URANS에서 난류 형태의 대류 롤이 발견된다는 사실 자체는 νt와 αt을 균질하다고 가정한 극도로 단순한 가상적 모델에서도 똑같이 관측될 것이다.

다음으로, 위 상황에 대한 대류 롤의 정략적인 유속 특성을 Remu~Ram0.45Prm-0.7으로 가정해보자. 여기서 첨자 m은 식 (4)에서 정의된 것과 똑같이, 무차원 수에 대한 정의에서 𝜈 및 𝛼가 각각 νe 및 αe로 도치되었음을 나타낸다. 위 관계식을 전개하면 가상-URANS에서 계산된 대류 롤의 유속을 특성을 다음과 같이 계산할 수 있다:

GDH 모델을 사용할 경우 νt≫ν 이면 νe/αe≈σT=0.9이기 때문에, 우리가 상정한 단순-URANS 모델에서는 모델이 예측하는 νt의 크기와 관계없이 원래의 비례관계 Reu~Ra0.45Pr-0.7를 상당히 비슷하게 재현할 수 있을 것으로 보인다. Kenjereš & Hanjalić[8,9,10,11]의 선행 URANS 연구에서 사용된 AFHM을 포함한 모델에서도 νe/ν와 αe/α가 근사적으로 비례할 것으로 예상되며, 이에 대한 정성적인 추정은 5절에서 제시될 예정이다. 이 AFHM을 사용한 URANS 모사에도, 비례관계 Reu~Ra0.45Pr-0.7이 상당히 비슷하게 재현될 수 있을 것으로 예측된다.

왜 이런 결과가 나왔는지를 이해하자면, 부력에 의한 자유 낙하 속도(free-fall velocity)를 살펴보아야 한다. 자유 낙하 속도 Uf는 부력에 의한 위치에너지 gβΔL가 운동에너지 u2/2으로 변환된다고 가정하면, 점성과 무관한 gβΔL~Uf2 의 관계식을 가정하여 얻어지는 속도이다. 이 식을 정리하면 UfL/ν≡Ref~Ra0.5Pr-0.5이 유도되며 이는 Reu~Ra0.45Pr-0.7의 관계식과 상당히 비슷하다. 즉, URANS에서 사용된 모델과 상관없이 대류 롤의 속도는 점성과 무관한 자유 낙하 속도만으로도 꽤 비슷하게 재현될 수 있다고 추정할 수 있다.

5. 대류 롤이 난류 열전달 예측에 미치는 영향

실제 RB 대류의 난류 열전달은 Nu=f(Ra,Pr)의 함수 관계로 정의될 수 있다. 기존 연구들에선 이 관계식에 대해 일반적으로 다음과 같은 멱법칙으로 표현한다:

여기서 상수 a, b, c는 Ra 및 Pr의 범위에 따라 달라진다[17]. 예를 들어, Garon et al.의 Pr≈0.7 및 10⁵≤Ra≤10⁹ 에 대한 실험에서는 Nu=0.123Ra0.294이 제안되었다[25]. Niemela et al.[26]의 헬륨 가스를 이용한 10⁸≤Ra≤10¹³, 049≤Pr≤14.72 범위의 실험 결과는 Nu=0.088Ra0.32으로 측정되었다.

이제 νt 및 αt가 균일한 가상적인 상황에선, 식 (4)에서 정의되는 Num, Ram, Prm의 관계를 식 (7)과 똑같이 Num=cRamaPrmb 으로 쓸 수 있다. 여기선 선행 연구에서 관측된 URANS의 유동 특성이 단순한 층류-대류 롤의 형태를 보이는 것이 아닌 복잡한 난류 대류의 경향성을 보이는 점에서, 난류 대류 영역의 멱법칙 관계식이 똑같이 연장되어 사용되었다.

이후 식 (4)를 식 (7)에 대입하면 URANS가 예측하는 열전달이 다음과 같이 정리된다:

실제 RB대류의 Ra 및 Pr의 범위, 및 URANS로 상사된 Ram, Prm의 범위가 모두 단일 멱법칙으로 표현된다고 가정하면, URANS가 정확한 답을 도출하기 위한 조건은 다음과 같다:

만약 Nu~Ra0.32Pr0 관계식을 대입하면 (νe/ν)=(αe/α)2.13을 얻을 수 있다. 식 (9)에서 URANS 결과의 정확성은 νe와 αe의 비율로 결정되며, 반면 난류 모델에서 예측된 νt값의 크기 자체와는 관련이 없다는 것을 유추할 수 있다. 극단적인 예시를 들자면, 만약 난류 모델이 νt=αt=0에 가깝게 매우 낮게 예측하는 상황을 상정해보자. 이 상황을 유체의 최소 움직임 단위까지 포착할 정도의 URANS를 수행한다면 이는 직접 수치 모사(direct numerical simulation)와 똑같아지며 모든 난류의 움직임은 포착되어 난류 열전달은 정확히 예측될 것이다.

다음으로 RB 대류를 URANS로 푸는 상황에서, 대류 롤의 존재를 가정한 뒤 난류 변수들의 예측에 미치는 영향을 추정해 보고자 한다. Kenjereš & Hanjalić의 선행연구[8]에서는 난류 열전달을 AHFM으로 모델링하며, k-ε-T'2¯의 난류 변수들에 대한 모델-전달방정식을 사용하였다. 이 모델들을 RB 대류에서 근사하면 다음과 같이 쓸 수 있다:

식 (10)는 순서대로 난류 점성, 난류 열전달에 대한 대수적 모델인 AHFM, 난류 운동에너지 k의 전달방정식, 온도 분산 T'2¯에 대한 전달방정식을 나타낸다. 모델 상수는 Cμ=0.03, Cθ=0.2, R=0.5, 𝜂=0.6의 값이 제안되었다. 본 연구의 분석에서는 대류 롤에 의한 난류 운동에너지 생성을 그 식의 정의에 따라 νt(U/L)2으로 추정하였다. 식 (10)에는 5개의 미지수 νt-αt-k-ε-T'2¯가 존재하며, 따라서 4개의 방정식을 정리할 경우 νt-αt에 대한 관계식을 도출할 수 있다:

여기서 Re는 대류 롤의 유속과 길이 특성을 나타내는 Reynolds 수이다. 여기서 4절에서 언급한 Reu~Ra0.45Pr-0.7을 대입하면, 우변 첫 항의 분모는 Ra-1PrRe2~Ra-0.1Pr-0.4으로 추정된다. 이를 대입하면, νt/αt~[1-ζRa-0.1Pr-0.4]으로, 여기서 𝜁는 모델 계수들과 Re의 멱법칙 계수들이 하나의 상수로 정리하여 표현한 값이다. 정리하자면, 식 (11)은 정성적으로 νt/αt가 넓은 Ra 및 Pr 범위에서 근사적으로 일정한 값을 가질 것으로 예측한다.

식 (9)과 νt/αt의 값이 일정할 것으로 추정하는 식 (11)이 서로 모순되지 않으려면, νt/ν와 αt/α가 근사적으로 Ra 및 Pr에 대해 거의 독립적인 값이 되어야 한다. νt/ν 및 αt/α가 근사적으로 상수 값을 가진다면, URANS에서 Ra 값이 커질수록 식 (5)에서 “모델의 효과(modeled effect, αe/α)”보다 “유체 움직임을 포착해 반영되는 열전달(resolved effect, Num)”의 효과가 더 주요해지게 된다. 2.2절에서 설명했듯이, Kenjereš & Hanjalić의 선행 연구에서는 Ra=10⁷, 10⁹의 두가지 케이스에서 URANS가 예측하는 열전달의 “모델 효과”와 “포착 효과”를 직접 비교하였다. 선행 연구 논문의 결과에서도 Ra가 커질수록 모델의 효과보다 URANS에서 직접 유체의 움직임을 포착하여 반영되는 열전달 효과가 더 커지는 것이 관찰되었다[11].

6. 결 론

Kenjereš & Hanjalić[8,9,10,11]의 선행 연구에서는 URANS는 성공적으로 RB대류의 난류 형태의 대류 롤을 캡쳐할 수 있으며, 이를 통해 정확한 난류 열전달을 예측할 수 있었다고 설명되었다. 하지만 RANS 모델 방정식의 복잡성 때문에 “어떻게 URANS가 대류 롤을 성공적으로 재현 할 수 있는지,” 그리고 “대류 롤이 URANS에서 예측되는 난류 열전달에 어떤 영향을 미치는지”에 대해선 구체적으로 분석된 바가 없었다. 본 연구의 목적은 URANS 시뮬레이션이 왜 그런 결과를 도출하는지를, 모델 방정식 그 자체로부터 유도된 분석적 추정을 통해 정성적으로 이해해 보는 것이다.

먼저, 실제 상황의 대류 롤의 유속은 점성과 상관없이 부력으로 인한 위치에너지가 운동에너지로 전환되는 자유 낙하 속도만으로도 비슷하게 추정할 수 있기 때문에, URANS에서 예측되는 대류 롤의 유속 특성은 난류 모델의 성능과 거의 관계없이 성공적으로 재현될 수 있을 것이라 설명되었다.

다음으로, URANS 계산에서 난류 형태의 대류 롤이 난류 열전달 예측에 미치는 영향을 분석하였다. URANS로 예측된 난류 열전달을 난류 모델이 기여하는 “모델 효과”와 유체 움직임으로 수송되는 열전달인 “포착 효과”로 나누었으며, 선행 URANS 연구들에서 Rayleigh 수가 커질수록 “모델 효과”의 기여율이 더 낮아지는 경향성을 설명하였다.

하지만 현재까지의 URANS 방법론에서는 어느 수준까지 유체를 직접 포착하는 것이 적절한 것 인가에 대한 명확한 학술적인 기준이 없다는 한계가 존재한다. 예를 들어, LES의 경우 격자의 크기를 inertial sub-range 안에 위치시킨 뒤 sub-grid 효과만 모델링하기 때문에 국소적인 모델의 유효성이 보장될 수 있다. 그러나, RANS의 경우 모델의 유효성은 일반적으로 모델이 정확하게 재현할 수 있는 제한된 몇 가지의 분석해(균질 전단 흐름, 균질 감쇠 흐름, log-law region 등)에 의해서만 경험적으로 검토되며, 이는 URANS 모사 방법을 정당화 하기 매우 어렵다. 특히 실제 RB 대류 문제에서는 두 수평 평판 사이의 길이와 비슷한 길이 규모를 가진 대류 롤로 난류의 특성이 주요하게 결정지어지지만, 높은 Rayleigh 수의 URANS 모사에서는 그보다 훨씬 작은 길이 규모에 대한 난류 확산도를 예측해 난류 효과를 모델링한다. 이러한 근본적인 한계점들은 향후 이 분야의 여러 연구자에 의한 심도 있는 토의를 통해 해결되어야 할 과제로 보인다.